【题目】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=![]() AD,∠BAD=∠ABC=90°,E是PD的中点.
AD,∠BAD=∠ABC=90°,E是PD的中点.
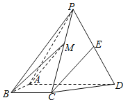
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.
参考答案:
【答案】(1)见解析(2)![]()
【解析】
(1)取PA的中点F,连接EF,BF,通过证明CE∥BF,利用直线与平面平行的判定定理证明即可.
(2)利用已知条件转化求解M到底面的距离,作出二面角的平面角,然后求解二面角M-AB-D的余弦值即可.
(1)证明:取PA的中点F,连接EF,BF,因为E是PD的中点,所以EF![]() AD,EF=
AD,EF=![]() AD,AB=BC=
AD,AB=BC=![]() AD,∠BAD=∠ABC=90°,∴BC
AD,∠BAD=∠ABC=90°,∴BC![]() EF, BC=EF
EF, BC=EF
∴BCEF是平行四边形,可得CE∥BF,BF平面PAB,CE平面PAB,
∴直线CE![]() 平面PAB;
平面PAB;
(2)解:四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=![]() AD,∠BAD=∠ABC=90°,E是PD的中点.
AD,∠BAD=∠ABC=90°,E是PD的中点.
取AD的中点O,M在底面ABCD上的射影N在OC上,设AD=2,则AB=BC=1,OP=![]() ,
,
∴∠PCO=60°,直线BM与底面ABCD所成角为45°,
可得:BN=MN,CN=![]() MN,BC=1,可得:1+
MN,BC=1,可得:1+![]() BN2=BN2,BN=
BN2=BN2,BN=![]() ,MN=
,MN=![]() ,
,
作NQ⊥AB于Q,连接MQ,AB⊥MN,所以∠MQN就是二面角M-AB-D的平面角,MQ=![]()
=![]() ,二面角M-AB-D的余弦值为:
,二面角M-AB-D的余弦值为:![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.

(1)求证:AB∥EF;
(2)若PA=AD,且平面PAD⊥平面ABCD,求证:AF⊥平面PCD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣(a+2)x+alnx,其中常数a>0.
(Ⅰ)当a>2时,求函数f(x)的单调递增区间;
(Ⅱ)设定义在D上的函数y=h(x)在点P(x0 , h(x0))处的切线方程为l:y=g(x),若 >0在D内恒成立,则称P为函数y=h(x)的“类对称点”.当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
>0在D内恒成立,则称P为函数y=h(x)的“类对称点”.当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
以直角坐标系xOy的原点为极点,x轴的非负半轴为极轴建立极坐标系,且两坐标系相同的长度单位.已知点N的极坐标为( ,
,  ),M是曲线C1:ρ=1上任意一点,点G满足
),M是曲线C1:ρ=1上任意一点,点G满足  ,设点G的轨迹为曲线C2 .
,设点G的轨迹为曲线C2 .
(1)求曲线C2的直角坐标方程;
(2)若过点P(2,0)的直线l的参数方程为 (t为参数),且直线l与曲线C2交于A,B两点,求
(t为参数),且直线l与曲线C2交于A,B两点,求  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的圆心坐标
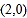 且与线y=3x+4相切,
且与线y=3x+4相切,(1)求圆C的方程;
(2)设直线
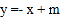 与圆C交于M,N两点,那么以MN为直径的圆能否经过原点,若能,请求出直线MN的方程;若不能,请说明理由.
与圆C交于M,N两点,那么以MN为直径的圆能否经过原点,若能,请求出直线MN的方程;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知定义在R上的函数f(x)=|x﹣m|+|x|,m∈N* , 存在实数x使f(x)<2成立.
(Ⅰ)求实数m的值;
(Ⅱ)若α,β>1,f(α)+f(β)=2,求证: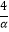 +
+ 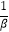 ≥
≥  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
 的图象向左平移
的图象向左平移 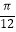 个单位,得到函数g(x)的图象,则下列关于g(x)叙述正确的是( )
个单位,得到函数g(x)的图象,则下列关于g(x)叙述正确的是( )
A.g(x)的最小正周期为2π
B.g(x)在 内单调递增
内单调递增
C.g(x)的图象关于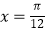 对称
对称
D.g(x)的图象关于 对称
对称
相关试题

