【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为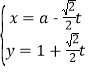 (
(![]() 为参数,
为参数,![]() ),以坐标原点为极点,以
),以坐标原点为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点(
两点(![]() 在
在![]() 之间),且
之间),且![]() ,求实数
,求实数![]() 的值.
的值.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】分析:(1)利用代入消参法,把曲线![]() 的参数方程化为普通方程,根据
的参数方程化为普通方程,根据![]() ,把曲线
,把曲线![]() 的极坐标方程转化为直角坐标方程;
的极坐标方程转化为直角坐标方程;
(2)将曲线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 得
得![]() , 设
, 设![]() 对应的参数为
对应的参数为![]() ,由题意得
,由题意得![]() 且
且![]() 在
在![]() 之间,则
之间,则![]() ,结合韦达定理可得实数
,结合韦达定理可得实数![]() 的值.
的值.
详解:(1)![]() 的参数方程
的参数方程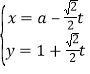 ,消参得普通方程为
,消参得普通方程为![]() ,
,
![]() 的极坐标方程为
的极坐标方程为![]() 两边同乘
两边同乘![]() 得
得![]() 即
即![]() .
.
(2)将曲线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 得
得![]() , 设
, 设![]() 对应的参数为
对应的参数为![]() ,由题意得
,由题意得![]() 且
且![]() 在
在![]() 之间,则
之间,则![]() ,
,
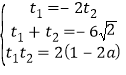 解得
解得![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某生物研究者于元旦在湖中放入一些凤眼莲,这些凤眼莲在湖中的蔓延速度越来越快,二月底测得凤眼莲覆盖面积为
 ,三月底测得凤眼莲覆盖面积为
,三月底测得凤眼莲覆盖面积为 ,凤眼莲覆盖面积
,凤眼莲覆盖面积 (单位:
(单位: )与月份
)与月份 (单位:月)的关系有两个函数模型
(单位:月)的关系有两个函数模型 与
与 可供选择.
可供选择.(1)试判断哪个函数模型更合适并求出该模型的解析式;
(2)求凤眼莲覆盖面积是元旦放入面积
 倍以上的最小月份.
倍以上的最小月份.(参考数据
 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的奇函数
上的奇函数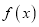 满足
满足 ,
,  为数列
为数列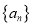 的前
的前 项和,且
项和,且 ,则
,则 __________.
__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】记
 分别为函数
分别为函数 的导函数.若存在
的导函数.若存在 ,满足
,满足 且
且 ,则称
,则称 为函数
为函数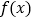 与
与 的一个“S点”.
的一个“S点”.(1)证明:函数
 与
与 不存在“S点”;
不存在“S点”;(2)若函数
 与
与 存在“S点”,求实数a的值;
存在“S点”,求实数a的值;(3)已知函数
 ,
, .对任意
.对任意 ,判断是否存在
,判断是否存在 ,使函数
,使函数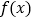 与
与 在区间
在区间 内存在“S点”,并说明理由.
内存在“S点”,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
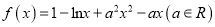 .
.(1)讨论函数
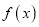 的单调性;
的单调性;(2)若
 且
且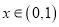 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如表所示:
组别
候车时间
人数
一

2
二
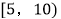
6
三
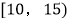
4
四
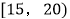
2
五
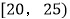
1
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自同一组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2017年种植的一批试验紫甘薯在温度升高时6组死亡的株数:

经计算:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,其中
,其中 分别为试验数据中的温度和死亡株数,
分别为试验数据中的温度和死亡株数,  .
.(1)若用线性回归模型,求
 关于
关于 的回归方程
的回归方程 (结果精确到
(结果精确到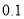 );
);(2)若用非线性回归模型求得
 关于
关于 的回归方程为
的回归方程为 ,且相关指数为
,且相关指数为 .
.(i)试与(1)中的回归模型相比,用
 说明哪种模型的拟合效果更好;
说明哪种模型的拟合效果更好;(ii)用拟合效果好的模型预测温度为
 时该批紫甘薯死亡株数(结果取整数).
时该批紫甘薯死亡株数(结果取整数).附:对于一组数据
 ,
,  ,……,
,……,  ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:  ;相关指数为:
;相关指数为:  .
.
相关试题

