【题目】记![]() 分别为函数
分别为函数![]() 的导函数.若存在
的导函数.若存在![]() ,满足
,满足![]() 且
且![]() ,则称
,则称![]() 为函数
为函数![]() 与
与![]() 的一个“S点”.
的一个“S点”.
(1)证明:函数![]() 与
与![]() 不存在“S点”;
不存在“S点”;
(2)若函数![]() 与
与![]() 存在“S点”,求实数a的值;
存在“S点”,求实数a的值;
(3)已知函数![]() ,
,![]() .对任意
.对任意![]() ,判断是否存在
,判断是否存在![]() ,使函数
,使函数![]() 与
与![]() 在区间
在区间![]() 内存在“S点”,并说明理由.
内存在“S点”,并说明理由.
参考答案:
【答案】(1)证明见解析
(2)a的值为![]()
(3)对任意a>0,存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”.
【解析】分析:(1)根据题中“S点”的定义列两个方程,根据方程组无解证得结论;(2)同(1)根据“S点”的定义列两个方程,解方程组可得a的值;(3)通过构造函数以及结合 “S点”的定义列两个方程,再判断方程组是否有解即可证得结论.
详解:解:(1)函数f(x)=x,g(x)=x2+2x-2,则f′(x)=1,g′(x)=2x+2.
由f(x)=g(x)且f′(x)= g′(x),得
![]() ,此方程组无解,
,此方程组无解,
因此,f(x)与g(x)不存在“S”点.
(2)函数![]() ,
,![]() ,
,
则![]() .
.
设x0为f(x)与g(x)的“S”点,由f(x0)与g(x0)且f′(x0)与g′(x0),得
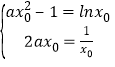 ,即
,即 ,(*)
,(*)
得![]() ,即
,即![]() ,则
,则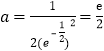 .
.
当![]() 时,
时,![]() 满足方程组(*),即
满足方程组(*),即![]() 为f(x)与g(x)的“S”点.
为f(x)与g(x)的“S”点.
因此,a的值为![]() .
.
(3)对任意a>0,设![]() .
.
因为![]() ,且h(x)的图象是不间断的,
,且h(x)的图象是不间断的,
所以存在![]() ∈(0,1),使得
∈(0,1),使得![]() ,令
,令![]() ,则b>0.
,则b>0.
函数![]() ,
,
则![]() .
.
由f(x)与g(x)且f′(x)与g′(x),得
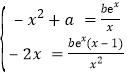 ,即
,即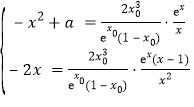 (**)
(**)
此时,![]() 满足方程组(**),即
满足方程组(**),即![]() 是函数f(x)与g(x)在区间(0,1)内的一个“S点”.
是函数f(x)与g(x)在区间(0,1)内的一个“S点”.
因此,对任意a>0,存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面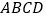 是平行四边形,
是平行四边形, 平面
平面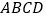 ,
, ,
, ,
,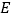 是棱
是棱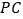 上的一点.
上的一点.(1)证明:
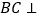 平面
平面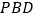 ;
; (2)若
 平面
平面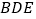 ,求
,求 的值;
的值;(3)在(2)的条件下,三棱锥
 的体积是18,求
的体积是18,求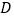 点到平面
点到平面 的距离.
的距离.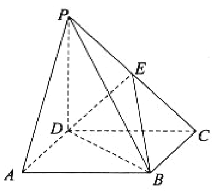
-
科目: 来源: 题型:
查看答案和解析>>【题目】某生物研究者于元旦在湖中放入一些凤眼莲,这些凤眼莲在湖中的蔓延速度越来越快,二月底测得凤眼莲覆盖面积为
 ,三月底测得凤眼莲覆盖面积为
,三月底测得凤眼莲覆盖面积为 ,凤眼莲覆盖面积
,凤眼莲覆盖面积 (单位:
(单位: )与月份
)与月份 (单位:月)的关系有两个函数模型
(单位:月)的关系有两个函数模型 与
与 可供选择.
可供选择.(1)试判断哪个函数模型更合适并求出该模型的解析式;
(2)求凤眼莲覆盖面积是元旦放入面积
 倍以上的最小月份.
倍以上的最小月份.(参考数据
 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在
 上的奇函数
上的奇函数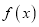 满足
满足 ,
,  为数列
为数列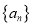 的前
的前 项和,且
项和,且 ,则
,则 __________.
__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
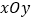 中,曲线
中,曲线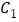 过点
过点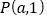 ,其参数方程为
,其参数方程为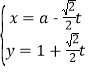 (
(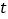 为参数,
为参数,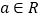 ),以坐标原点为极点,以
),以坐标原点为极点,以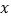 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线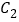 的极坐标方程为
的极坐标方程为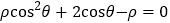 .
.(1)写出曲线
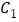 的普通方程和曲线
的普通方程和曲线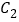 的直角坐标方程;
的直角坐标方程;(2)已知曲线
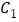 和曲线
和曲线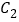 交于
交于 两点(
两点(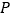 在
在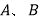 之间),且
之间),且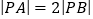 ,求实数
,求实数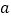 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
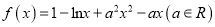 .
.(1)讨论函数
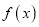 的单调性;
的单调性;(2)若
 且
且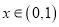 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如表所示:
组别
候车时间
人数
一

2
二
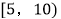
6
三
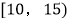
4
四
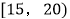
2
五
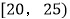
1
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自同一组的概率.
相关试题

