【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() 且
且![]() ,求证:
,求证: ![]() .
.
参考答案:
【答案】(1)答案见解析;(2)证明见解析.
【解析】试题分析:(1)对函数求导,然后分类讨论若![]() 时、
时、![]() 时和
时和![]() 时三种情况,分别给出单调性(2)法一:构造
时三种情况,分别给出单调性(2)法一:构造![]() ,求导算出最值
,求导算出最值![]() ,构造
,构造![]() ,利用二阶导数,得
,利用二阶导数,得![]() ,从而得证;法二:利用放缩法当
,从而得证;法二:利用放缩法当![]() 时,得
时,得![]() ,即
,即![]() ,然后再证明;法三:对问题放缩由于
,然后再证明;法三:对问题放缩由于![]() ,则只需证明
,则只需证明![]() ,然后给出证明
,然后给出证明
解析:解法一:(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
①若![]() 时,则
时,则![]() ,
, ![]() 在
在![]() 上单调递减;
上单调递减;
②若![]() 时,当
时,当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() .
.
故在![]() 上,
上, ![]() 单调递减;在
单调递减;在![]() 上,
上, ![]() 单调递増;
单调递増;
③若![]() 时,当
时,当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
故在![]() 上,
上, ![]() 单调递减;在
单调递减;在![]() 上,
上, ![]() 单调递増.
单调递増.
(2)若![]() 且
且![]() ,
,
欲证![]() ,
,
只需证![]() ,
,
即证![]() .
.
设函数![]() ,则
,则![]() .
.
当![]() 时,
时, ![]() .故函数
.故函数![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() .
.
设函数![]() ,则
,则![]() .
.
设函数![]() ,则
,则![]() .
.
当![]() 时,
时, ![]() ,
,
故存在![]() ,使得
,使得![]() ,
,
从而函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减.
上单调递减.
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]()
故存在![]() ,使得
,使得![]() ,
,
即当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]()
从而函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减.
上单调递减.
因为![]() ,
,
故当![]() 时,
时, ![]()
所以![]() ,
,
即![]() .
.
解法二:(1)同解法一.
(2)若![]() 且
且![]() ,
,
欲证![]() ,
,
只需证![]() ,
,
即证![]() .
.
设函数![]() ,则
,则![]() .
.
当![]() 时,
时, ![]() .故函数
.故函数![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() .
.
设函数![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以![]() ,
,
即原不等式成立.
解法三:(1)同解法一.
(2)若![]() 且
且![]() ,
,
欲证![]() ,
,
只需证![]() ,
,
由于![]() ,则只需证明
,则只需证明![]() ,
,
只需证明![]() ,令
,令![]() ,
,
则![]() ,
,
则函数![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,
,
所以![]() 成立,
成立,
即原不等式成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
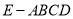 中,
中, 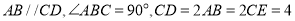 ,
,  .
.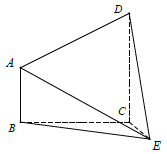
(1)证明:平面
 平面
平面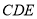 ;
;(2)若
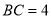 ,求二面角
,求二面角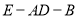 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我校为了让高一学生更有效率地利用周六的时间,在高一新生第一次摸底考试后采取周六到校自主学习,同时由班主任老师值班,家长轮流值班.一个月后进行了第一次月考,高一数学教研组通过系统抽样抽取了
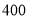 名学生,并统计了他们这两次数学考试的优良人数和非优良人数,其中部分统计数据如下:
名学生,并统计了他们这两次数学考试的优良人数和非优良人数,其中部分统计数据如下:
(1)请画出这次调查得到的
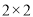 列联表;并判定能否在犯错误概率不超过
列联表;并判定能否在犯错误概率不超过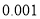 的前提下认为周六到校自习对提高学生成绩有效?
的前提下认为周六到校自习对提高学生成绩有效?(2)从这组学生摸底考试中数学优良成绩中和第一次月考的数学非优良成绩中,按分层抽样随机抽取
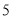 个成绩,再从这
个成绩,再从这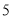 个成绩中随机抽取
个成绩中随机抽取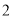 个,求这
个,求这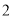 个成绩来自同一次考试的概率.
个成绩来自同一次考试的概率.下面是临界值表供参考:

(参考公式:
 ,其中
,其中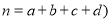
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
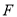 为椭圆
为椭圆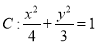 的右焦点,
的右焦点, 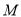 为
为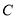 上的任意一点.
上的任意一点. (1)求
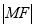 的取值范围;
的取值范围;(2)
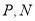 是
是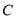 上异于
上异于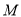 的两点,若直线
的两点,若直线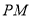 与直线
与直线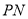 的斜率之积为
的斜率之积为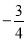 ,证明:
,证明: 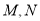 两点的横坐标之和为常数.
两点的横坐标之和为常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018届福建省福州市高三上学期期末】过椭圆
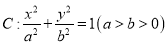 的右焦点作
的右焦点作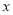 轴的垂线,交
轴的垂线,交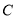 于
于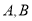 两点,直线
两点,直线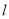 过
过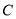 的左焦点和上顶点.若以
的左焦点和上顶点.若以 为直径的圆与
为直径的圆与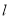 存在公共点,则
存在公共点,则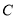 的离心率的取值范围是( )
的离心率的取值范围是( )A.
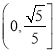 B.
B. 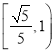 C.
C. 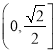 D.
D. 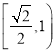
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为
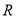 的函数
的函数 是奇函数.
是奇函数.(1)求
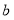 的值;
的值;(2)判断函数
 的单调性,并用定义证明;
的单调性,并用定义证明;(3)当
 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
分组
频数
频率
50.5~60.5
4
0.08
60.5~70.5
0.16
70.5~80.5
10
80.5~90.5
16
0.32
90.5~100.5
合计
50
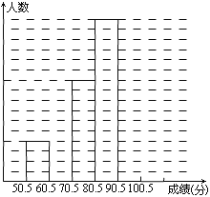
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
相关试题

