【题目】如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6 ![]() ,则BC的长为 .
,则BC的长为 . 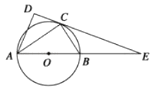
参考答案:
【答案】2 ![]()
【解析】解:连接OC,在直角三角形ACB和ADC中,
∠D=∠ACB,∠CAB=∠DAC,
可得∠DCA=∠CBA,
又OB=OC,即∠CBA=∠BCO,
又∠BCO+∠ACO=90°,
可得∠DCA+∠ACO=90°,
即有OC⊥DE,ED为圆O的切线,
由圆的切割线定理,可得CE2=BEAE,
即有(6 ![]() )2=6(6+AB),
)2=6(6+AB),
解得AB=6,即圆的半径为3,
由AD∥OC,可得 ![]() =
= ![]() ,
,
即为 ![]() =
= ![]() ,即有CD=2
,即有CD=2 ![]() ,
,
又 ![]() =
= ![]() ,即为
,即为 ![]() =
= ![]() ,
,
解得AD=4,AC= ![]() =2
=2 ![]() ,
,
BC= ![]() =
= ![]() =2
=2 ![]() .
.
所以答案是:2 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,下列结论中错误的是
,下列结论中错误的是A.

 , f(
, f( )=0
)=0B. 函数y=f(x)的图像是中心对称图形
C. 若
 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞, )单调递减
)单调递减D. 若
 是f(x)的极值点,则
是f(x)的极值点,则 (
( )=0
)=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的公差d≠0,且a1 , a3 , a13成等比数列,若a1=1,Sn是数列{an}前n项的和,则
 (n∈N+)的最小值为( )
(n∈N+)的最小值为( )
A.4
B.3
C.2 ﹣2
﹣2
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)在R上存在导数f′(x),对任意的x∈R,有f(﹣x)+f(x)=x2 , 且x∈(0,+∞)时,f′(x)>x.若f(2﹣a)﹣f(a)≥2﹣2a,则实数a的取值范围为( )
A.[1,+∞)
B.(﹣∞,1]
C.(﹣∞,2]
D.[2,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=1,AD=
 ,P矩形内的一点,且AP=
,P矩形内的一点,且AP=  ,若
,若 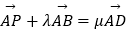 ,(λ,μ∈R),則λ+
,(λ,μ∈R),則λ+  μ的最大值为 .
μ的最大值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=sin(
 x﹣
x﹣  )﹣2cos2
)﹣2cos2  x+1.
x+1.
(1)求f(x)的最小正周期;
(2)若函数y=f(x)与y=g(x)的图象关于直线x=1对称,求当x∈[0, ]时,y=g(x)的最大值.
]时,y=g(x)的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率;
(Ⅱ)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列与数学期望Eξ.
相关试题

