【题目】设函数f(x)在R上存在导数f′(x),对任意的x∈R,有f(﹣x)+f(x)=x2 , 且x∈(0,+∞)时,f′(x)>x.若f(2﹣a)﹣f(a)≥2﹣2a,则实数a的取值范围为( )
A.[1,+∞)
B.(﹣∞,1]
C.(﹣∞,2]
D.[2,+∞)
参考答案:
【答案】B
【解析】解:∵f(﹣x)+f(x)=x2 , ∴f(x)﹣ ![]() x2 +f(﹣x)﹣
x2 +f(﹣x)﹣ ![]() x2 =0,
x2 =0,
令g(x)=f(x)﹣ ![]() x2 , ∵g(﹣x)+g(x)=f(﹣x)﹣
x2 , ∵g(﹣x)+g(x)=f(﹣x)﹣ ![]() x2+f(x)﹣
x2+f(x)﹣ ![]() x2=0,
x2=0,
∴函数g(x)为奇函数.
∵x∈(0,+∞)时,f′(x)>x.
∴x∈(0,+∞)时,g′(x)=f′(x)﹣x>0,故函数g(x)在(0,+∞)上是增函数,
故函数g(x)在(﹣∞,0)上也是增函数,由f(0)=0,可得g(x)在R上是增函数.
f(2﹣a)﹣f(a)≥2﹣2a,等价于f(2﹣a)﹣ ![]() ≥f(a)﹣
≥f(a)﹣ ![]() ,
,
即g(2﹣a)≥g(a),∴2﹣a≥a,解得a≤1,
故选:B.
【考点精析】关于本题考查的基本求导法则,需要了解若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(1)当
 时,求函数
时,求函数 的单调区间.
的单调区间.(2)当
 时,讨论函数
时,讨论函数 与
与 图象的交点个数.
图象的交点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,下列结论中错误的是
,下列结论中错误的是A.

 , f(
, f( )=0
)=0B. 函数y=f(x)的图像是中心对称图形
C. 若
 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞, )单调递减
)单调递减D. 若
 是f(x)的极值点,则
是f(x)的极值点,则 (
( )=0
)=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的公差d≠0,且a1 , a3 , a13成等比数列,若a1=1,Sn是数列{an}前n项的和,则
 (n∈N+)的最小值为( )
(n∈N+)的最小值为( )
A.4
B.3
C.2 ﹣2
﹣2
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6
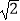 ,则BC的长为 .
,则BC的长为 . 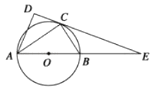
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=1,AD=
 ,P矩形内的一点,且AP=
,P矩形内的一点,且AP=  ,若
,若 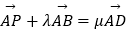 ,(λ,μ∈R),則λ+
,(λ,μ∈R),則λ+  μ的最大值为 .
μ的最大值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=sin(
 x﹣
x﹣  )﹣2cos2
)﹣2cos2  x+1.
x+1.
(1)求f(x)的最小正周期;
(2)若函数y=f(x)与y=g(x)的图象关于直线x=1对称,求当x∈[0, ]时,y=g(x)的最大值.
]时,y=g(x)的最大值.
相关试题

