【题目】【2017山西三区八校二模】已知函数![]() (其中
(其中![]() ,
, ![]() 为常数且
为常数且![]() )在
)在![]() 处取得极值.
处取得极值.
(Ⅰ)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 在
在![]() 上的最大值为1,求
上的最大值为1,求![]() 的值.
的值.
参考答案:
【答案】(Ⅰ)单调递增区间为![]() ,
, ![]() ;单调递减区间为
;单调递减区间为![]() ; (Ⅱ)
; (Ⅱ)![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)由函数的解析式,可求出函数导函数的解析式,进而根据![]() 是
是![]() 的一个极值点
的一个极值点![]() ,可构造关于
,可构造关于![]() ,
, ![]() 的方程,根据
的方程,根据![]() 求出
求出![]() 值;可得函数导函数的解析式,分析导函数值大于0和小于0时,
值;可得函数导函数的解析式,分析导函数值大于0和小于0时, ![]() 的范围,可得函数
的范围,可得函数![]() 的单调区间;
的单调区间;
(Ⅱ)对函数求导,写出函数的导函数等于0的![]() 的值,列表表示出在各个区间上的导函数和函数的情况,做出极值,把极值同端点处的值进行比较得到最大值,最后利用条件建立关于
的值,列表表示出在各个区间上的导函数和函数的情况,做出极值,把极值同端点处的值进行比较得到最大值,最后利用条件建立关于![]() 的方程求得结果.
的方程求得结果.
试题解析:
(Ⅰ)因为![]() ,所以
,所以![]() ,
,
因为函数![]() 在
在![]() 处取得极值,
处取得极值,
![]()
当![]() 时,
时, ![]() ,
, ![]() ,
,
由![]() ,得
,得![]() 或
或![]() ;由
;由![]() ,得
,得![]() ,
,
即函数![]() 的单调递增区间为
的单调递增区间为![]() ,
, ![]() ;单调递减区间为
;单调递减区间为![]() .
.
(Ⅱ)因为![]() ,
,
令![]() ,
, ![]() ,
, ![]() ,
,
因为![]() 在
在![]() 处取得极值,所以
处取得极值,所以![]() ,
,
当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增, ![]() 上单调递减,
上单调递减, ![]() 上单调递增,
上单调递增,
所以最大值1可能的在![]() 或
或![]() 处取得,而
处取得,而![]()
![]()
![]() ,
,
所以![]() ,解得
,解得![]() ;
;
当![]() 时,
时, ![]() 在区间
在区间![]() 上单调递增,
上单调递增, ![]() 上单调递减,
上单调递减, ![]() 上单调递增,
上单调递增,
所以最大值1可能在![]() 或
或![]() 处取得,
处取得,
而![]() ,
,
所以![]() ,
,
解得![]() ,与
,与![]() 矛盾.
矛盾.
当![]() 时,
时, ![]() 在区间
在区间![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所最大值1可能在![]() 处取得,而
处取得,而![]() ,矛盾.
,矛盾.
综上所述, ![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园,种植桃树,已知角A为120°.现在边界AP,AQ处建围墙,PQ处围栅栏.

(1)若∠APQ=15°,AP与AQ两处围墙长度和为100(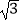 +1)米,求栅栏PQ的长;
+1)米,求栅栏PQ的长;
(2)已知AB,AC的长度均大于200米,若水果园APQ面积为2500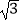 平方米,问AP,AQ长各为多少时,可使三角形APQ周长最小?
平方米,问AP,AQ长各为多少时,可使三角形APQ周长最小? -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A、B、C所对的边长分别为a,b,c且满足csinA=
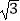 acosC,则sinA+sinB的最大值是( )
acosC,则sinA+sinB的最大值是( )
A.1
B.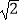
C.3
D.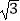
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x|x﹣a|,a∈R,g(x)=x2﹣1.
(1)当a=1时,解不等式f(x)≥g(x);
(2)记函数f(x)在区间[0,2]上的最大值为F(a),求F(a)的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017山西孝义考前热身】已知函数
 (
(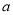 是常数),
是常数),(1)求函数
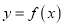 的单调区间;
的单调区间;(2)当
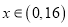 时,函数
时,函数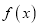 有零点,求
有零点,求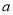 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足:a4=7,a10=19,其前n项和为Sn .
(1)求数列{an}的通项公式an及Sn;
(2)若等比数列{bn}的前n项和为Tn , 且b1=2,b4=S4 , 求Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】Sn为数列的前n项和,已知an>0,an2+2an=4Sn﹣1.
(1)求{an}的通项公式;
(2)求{an}的前n项和Sn .
相关试题

