【题目】在四边形ABCD中,已知 ![]() ∥
∥ ![]() ,
, ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3).
=(﹣2,﹣3).
(1)求用x表示y的关系式;
(2)若 ![]() ⊥
⊥ ![]() ,求x、y值.
,求x、y值.
参考答案:
【答案】
(1)解:∵ ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3),
=(﹣2,﹣3),
∴ ![]()
∵ ![]() ,
,
∴x(﹣2+y)=y(4+x)
∴y=﹣ ![]()
(2)解:∵ ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3),
=(﹣2,﹣3),
∴ ![]() =(x+6,y+1),
=(x+6,y+1),
![]() =(x﹣2,y﹣3),
=(x﹣2,y﹣3),
∵ ![]() ,
,
∴(x+6)(x﹣2)+(y+1)(y﹣3)=0,
又∵y=﹣ ![]() ,
,
解得 ![]() 或
或 ![]()
【解析】(1) ![]() ,由
,由 ![]() ,能求出y=﹣
,能求出y=﹣ ![]() .(2)
.(2) ![]() =(x+6,y+1),
=(x+6,y+1), ![]() =(x﹣2,y﹣3),由
=(x﹣2,y﹣3),由 ![]() ,y=﹣
,y=﹣ ![]() ,能求出x、y值.
,能求出x、y值.
【考点精析】掌握数量积判断两个平面向量的垂直关系是解答本题的根本,需要知道若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ;即:两平面垂直
;即:两平面垂直![]() 两平面的法向量垂直.
两平面的法向量垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系如图一的一条折线表示;西红柿的种植成本与上市时间的关系如图二的抛物线段表示.
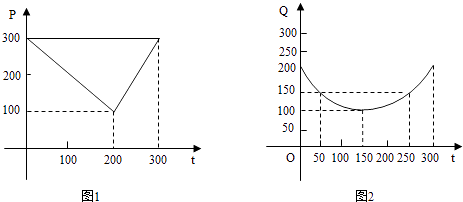
(1)写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价各种植成本的单位:元/102㎏,时间单位:天) -
科目: 来源: 题型:
查看答案和解析>>【题目】若命题p:曲线
 =1为双曲线,命题q:函数f(x)=(4﹣a)x在R上是增函数,且p∨q为真命题,p∧q为假命题,则实数a的取值范围是 .
=1为双曲线,命题q:函数f(x)=(4﹣a)x在R上是增函数,且p∨q为真命题,p∧q为假命题,则实数a的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
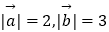 ,
, 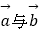 的夹角为60°,
的夹角为60°, 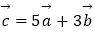 ,
, 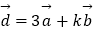 ,当实数k为何值时,
,当实数k为何值时,
(1)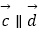
(2)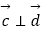 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
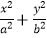 =1(a>b>0)上的动点到焦点距离的最小值为
=1(a>b>0)上的动点到焦点距离的最小值为 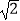 -1.以原点为圆心、椭圆的短半轴长为半径的圆与直线x﹣y+
-1.以原点为圆心、椭圆的短半轴长为半径的圆与直线x﹣y+ 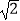 =0相切.
=0相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若过点M(2,0)的直线与椭圆C相交于A,B两点,P为椭圆上一点,且满足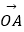 +
+ 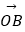 =t
=t 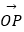 (O为坐标原点).当|AB|=
(O为坐标原点).当|AB|= 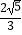 时,求实数t的值.
时,求实数t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
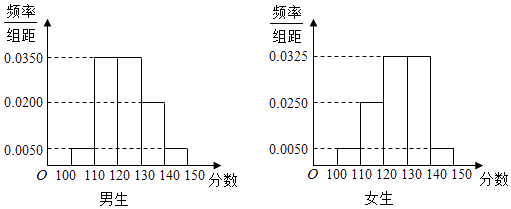
附:K2=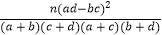 .
.
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?P(K2≥k0)
0.100
0.050
0.010
0.001
k0
2.706
3.841
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
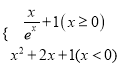 ,若函数y=f(f(x)﹣a)﹣1有三个零点,则a的取值范围是_____.
,若函数y=f(f(x)﹣a)﹣1有三个零点,则a的取值范围是_____.
相关试题

