【题目】若命题p:曲线 ![]() =1为双曲线,命题q:函数f(x)=(4﹣a)x在R上是增函数,且p∨q为真命题,p∧q为假命题,则实数a的取值范围是 .
=1为双曲线,命题q:函数f(x)=(4﹣a)x在R上是增函数,且p∨q为真命题,p∧q为假命题,则实数a的取值范围是 .
参考答案:
【答案】(﹣∞,2]∪[3,6)
【解析】解:当p为真命题时,(a﹣2)(6﹣a)>0,解之得2<a<6.当q为真命题时,4﹣a>1,即a<3.
由p∨q为真命题,p∧q为假命题知p、q一真一假.
当p真q假时,3≤a<6.当p假q真时,a≤2.
因此实数a的取值范围是(﹣∞,2]∪[3,6).
所以答案是:(﹣∞,2]∪[3,6).
【考点精析】通过灵活运用复合命题的真假,掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|2﹣5≤2﹣x≤4},B={x|x2+2mx﹣3m2<0,m>0}.
(1)若m=2,求A∩B;
(2)若BA,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知0<a<1,函数f(x)=loga(ax﹣1)
(I)求函数f(x)的定义域;
(Ⅱ)判断f(x)的单调性;
(Ⅲ)若m满足f(1﹣m)≥f(1﹣m2),求m的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系如图一的一条折线表示;西红柿的种植成本与上市时间的关系如图二的抛物线段表示.
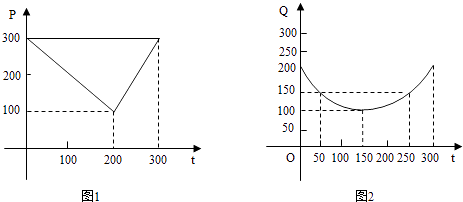
(1)写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价各种植成本的单位:元/102㎏,时间单位:天) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
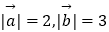 ,
, 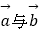 的夹角为60°,
的夹角为60°, 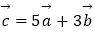 ,
, 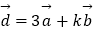 ,当实数k为何值时,
,当实数k为何值时,
(1)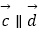
(2)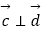 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,已知
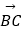 ∥
∥ 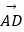 ,
, 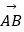 =(6,1),
=(6,1), 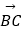 =(x,y),
=(x,y),  =(﹣2,﹣3).
=(﹣2,﹣3).
(1)求用x表示y的关系式;
(2)若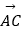 ⊥
⊥ 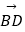 ,求x、y值.
,求x、y值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
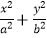 =1(a>b>0)上的动点到焦点距离的最小值为
=1(a>b>0)上的动点到焦点距离的最小值为 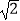 -1.以原点为圆心、椭圆的短半轴长为半径的圆与直线x﹣y+
-1.以原点为圆心、椭圆的短半轴长为半径的圆与直线x﹣y+ 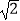 =0相切.
=0相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若过点M(2,0)的直线与椭圆C相交于A,B两点,P为椭圆上一点,且满足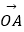 +
+ 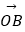 =t
=t 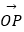 (O为坐标原点).当|AB|=
(O为坐标原点).当|AB|= 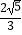 时,求实数t的值.
时,求实数t的值.
相关试题

