【题目】已知函数f(x)=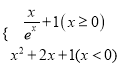 ,若函数y=f(f(x)﹣a)﹣1有三个零点,则a的取值范围是_____.
,若函数y=f(f(x)﹣a)﹣1有三个零点,则a的取值范围是_____.
参考答案:
【答案】![]()
【解析】当x<0时,由f(x)﹣1=0得x2+2x+1=1,得x=﹣2或x=0,
当x≥0时,由f(x)﹣1=0得![]() ,得x=0,
,得x=0,
由,y=f(f(x)﹣a)﹣1=0得f(x)﹣a=0或f(x)﹣a=﹣2,
即f(x)=a,f(x)=a﹣2,
作出函数f(x)的图象如图:
y=![]() ≥1(x≥0),
≥1(x≥0),
y′=![]() ,当x∈(0,1)时,y′>0,函数是增函数,x∈(1,+∞)时,y′<0,函数是减函数,
,当x∈(0,1)时,y′>0,函数是增函数,x∈(1,+∞)时,y′<0,函数是减函数,
x=1时,函数取得最大值: ![]() ,
,
当1<a﹣2![]() 时,即a∈(3,3+
时,即a∈(3,3+![]() )时,y=f(f(x)﹣a)﹣1有4个零点,
)时,y=f(f(x)﹣a)﹣1有4个零点,
当a﹣2=1+![]() 时,即a=3+
时,即a=3+![]() 时则y=f(f(x)﹣a)﹣1有三个零点,
时则y=f(f(x)﹣a)﹣1有三个零点,
当a>3+![]() 时,y=f(f(x)﹣a)﹣1有1个零点
时,y=f(f(x)﹣a)﹣1有1个零点
当a=1+![]() 时,则y=f(f(x)﹣a)﹣1有三个零点,
时,则y=f(f(x)﹣a)﹣1有三个零点,
当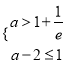 时,即a∈(1+
时,即a∈(1+![]() ,3)时,y=f(f(x)﹣a)﹣1有三个零点.
,3)时,y=f(f(x)﹣a)﹣1有三个零点.
综上a∈![]() ,函数有3个零点.
,函数有3个零点.
故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,已知
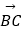 ∥
∥ 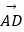 ,
, 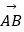 =(6,1),
=(6,1), 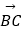 =(x,y),
=(x,y),  =(﹣2,﹣3).
=(﹣2,﹣3).
(1)求用x表示y的关系式;
(2)若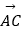 ⊥
⊥ 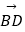 ,求x、y值.
,求x、y值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
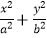 =1(a>b>0)上的动点到焦点距离的最小值为
=1(a>b>0)上的动点到焦点距离的最小值为 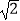 -1.以原点为圆心、椭圆的短半轴长为半径的圆与直线x﹣y+
-1.以原点为圆心、椭圆的短半轴长为半径的圆与直线x﹣y+ 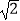 =0相切.
=0相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若过点M(2,0)的直线与椭圆C相交于A,B两点,P为椭圆上一点,且满足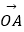 +
+ 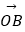 =t
=t 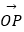 (O为坐标原点).当|AB|=
(O为坐标原点).当|AB|= 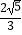 时,求实数t的值.
时,求实数t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
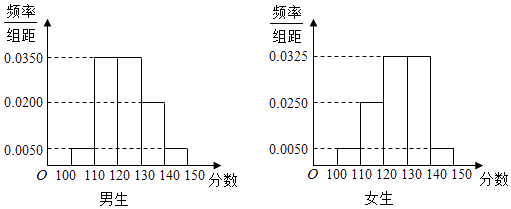
附:K2=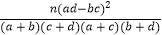 .
.
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?P(K2≥k0)
0.100
0.050
0.010
0.001
k0
2.706
3.841
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y2=2px(p>0)上的一点M的横坐标为3,焦点为F,且|MF|=4.直线l:y=2x﹣4与抛物线C交于A,B两点.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若P是x轴上一点,且△PAB的面积等于9,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)满足以下条件:①定义在正实数集上;②f(
 )=2;③对任意实数t,都有f(xt)=tf(x)(x∈R+).
)=2;③对任意实数t,都有f(xt)=tf(x)(x∈R+).
(1)求f(1),f( )的值;
)的值;
(2)求证:对于任意x,y∈R+ , 都有f(xy)=f(x)+f(y);
(3)若不等式f(loga(x﹣3a)﹣1)﹣f(﹣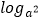
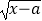 )≥﹣4对x∈[a+2,a+
)≥﹣4对x∈[a+2,a+  ]恒成立,求实数a的取值范围.
]恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在直三棱柱ABC﹣A1B1C1中,AB=AA1=2,∠ABC=90°,点E、F分别是棱AB、BB1的中点,当二面角C1﹣AA1﹣B为45o时,直线EF和BC1所成的角为( )
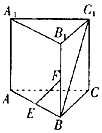
A.45o
B.60o
C.90o
D.120o
相关试题

