【题目】已知中心在坐标原点,焦点在![]() 轴上的椭圆,离心率为
轴上的椭圆,离心率为![]() 且过点
且过点![]() ,过定点
,过定点![]() 的动直线与该椭圆相交于
的动直线与该椭圆相交于![]() 、
、![]() 两点.
两点.
(1)若线段![]() 中点的横坐标是
中点的横坐标是![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为常数?若存在,求出点
为常数?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)椭圆的离心率公式,及![]() 的关系,求得
的关系,求得![]() ,得到椭圆的方程;设出直线
,得到椭圆的方程;设出直线![]() 的方程,将直线方程代入椭圆,用舍而不求和韦达定理方法表示出中点坐标,此时代入已知
的方程,将直线方程代入椭圆,用舍而不求和韦达定理方法表示出中点坐标,此时代入已知![]() 中点的横坐标,即可求出直线
中点的横坐标,即可求出直线![]() 的方程;(2)假设存在点
的方程;(2)假设存在点![]() ,使
,使![]() 为常数,分别分当
为常数,分别分当![]() 与
与![]() 轴不垂直时以及当直线
轴不垂直时以及当直线![]() 与
与![]() 轴垂直时,求出点
轴垂直时,求出点![]() 的坐标,最后综合两种情况得出结论.
的坐标,最后综合两种情况得出结论.
试题解析:(1)易求椭圆的方程为![]() ,
,
直线斜率不存在时显然不成立,设直线![]() ,
,
将![]() 代入椭圆的方程
代入椭圆的方程![]() ,
,
消去![]() 整理得
整理得![]() ,
,
设![]() ,则
,则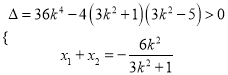 ,
,
因为线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,解得
,解得![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.
(2)假设在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() 为常数,
为常数,
①当直线![]() 与
与![]() 轴不垂直时,由(1)知
轴不垂直时,由(1)知![]() ,
,
所以![]()
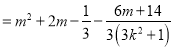 ,
,
因为![]() 是与
是与![]() 无关的常数,从而有
无关的常数,从而有![]() ,
,
此时![]()
②当直线![]() 与
与![]() 轴垂直时,此时结论成立,
轴垂直时,此时结论成立,
综上可知,在![]() 轴上存在定点
轴上存在定点![]() ,使
,使![]() ,为常数
,为常数
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
以坐标原点为极点,以
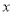 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线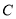 的参数方程为
的参数方程为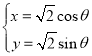 (
(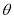 为参数,
为参数,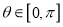 ),直线
),直线 的参数方程为
的参数方程为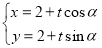 (
(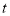 为参数).
为参数).(1)点
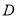 在曲线
在曲线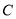 上,且曲线
上,且曲线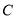 在点
在点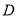 处的切线与直线
处的切线与直线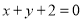 垂直,求点
垂直,求点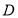 的极坐标;
的极坐标;(2)设直线
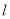 与曲线
与曲线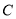 有两个不同的交点,求直线
有两个不同的交点,求直线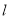 的斜率的取值范围.
的斜率的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1 ,正方形
 的边长为
的边长为 分别是
分别是 和
和 的中点,
的中点, 是正方形的对角线
是正方形的对角线 与
与 的交点,
的交点, 是正方形两对角线的交点,现沿
是正方形两对角线的交点,现沿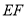 将
将 折起到
折起到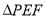 的位置,使得
的位置,使得 ,连结
,连结 (如图2).
(如图2).
(1)求证:
 ;
;(2)求三棱锥
 的高.
的高. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
 .
.(1)当
 时,解不等式
时,解不等式 ;
;(2)若
 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 ,圆
,圆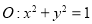 .
.(1)若抛物线
 的焦点
的焦点 在圆上,且
在圆上,且 为
为  和圆
和圆  的一个交点,求
的一个交点,求 ;
;(2)若直线
 与抛物线
与抛物线 和圆
和圆 分别相切于点
分别相切于点 ,求
,求 的最小值及相应
的最小值及相应 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为
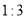 ,且成绩分布在
,且成绩分布在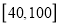 ,分数在
,分数在 以上(含
以上(含 )的同学获奖. 按文理科用分层抽样的方法抽取
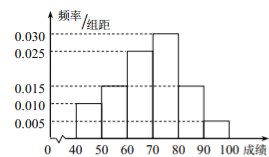
)的同学获奖. 按文理科用分层抽样的方法抽取 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).(1)填写下面的
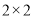 列联表,能否有超过
列联表,能否有超过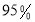 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?(2)将上述调査所得的频率视为概率,现从参赛学生中,任意抽取
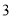 名学生,记“获奖”学生人数为
名学生,记“获奖”学生人数为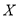 ,求
,求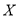 的分布列及数学期望.
的分布列及数学期望.文科生
理科生
合计
获奖
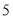
不获奖
合计

附表及公式:
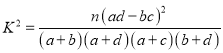 ,其中
,其中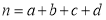
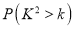

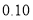

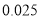
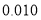
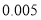
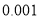
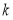
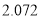

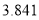
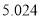
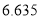
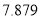
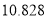
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 为偶函数,且函数
为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
.(1)求
 的值;
的值;(2)函数
 的图象向右平移
的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数 的图象,求
的图象,求 的单调递减区间.
的单调递减区间.
相关试题

