【题目】已知函数![]() .
.
(1)若![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(2)曲线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,其中
两点,其中![]() ,若直线
,若直线![]() 斜率为
斜率为![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】见解析
【解析】(1)![]() ,
,![]() (
(![]() ),当
),当![]() 时,恒有
时,恒有![]() ,
,![]() 在区间
在区间![]() 内是增函数; 当
内是增函数; 当![]() 时,令
时,令![]() ,即
,即![]() ,解得
,解得![]() ,令
,令![]() ,即
,即![]() ,解得
,解得![]() ,综上,当
,综上,当![]() 时,
时,![]() 在区间
在区间![]() 内是增函数;当
内是增函数;当![]() 时,
时,![]() 在
在 内是增函数,在
内是增函数,在 内是减函数.………………5分
内是减函数.………………5分
(2)证明:![]() ,要证明
,要证明![]() ,
,
即证![]() ,等价于
,等价于 ,令
,令![]() (由
(由![]() ,知
,知![]() ),
),
则只需证![]() ,由
,由![]() ,知
,知![]() ,故等价于
,故等价于![]() (
(![]() )(
)(![]() ). ……7分
). ……7分
①令![]() (
(![]() ),则
),则![]() (
(![]() ),所以
),所以![]() 在
在![]() 内是增函数,当
内是增函数,当![]() 时,
时, ![]() ,所以
,所以![]() ;
;
②令![]() (
(![]() ),则
),则![]() (
(![]() ),所以
),所以![]() 在
在![]() 内是增函数,所以当
内是增函数,所以当![]() 时,
时,![]() ,即
,即![]() (
(![]() ).
).
由②知(![]() )成立,所以
)成立,所以![]() .……12分
.……12分
请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
【命题意图】本题考查利用导数求函数的单调性、极值、最值,函数与方程、不等式等基础知识,意在考查学生的综合分析问题、解决问题的能力和基本运算能力.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙二人参加普法知识竞答,共有10个不同的题目,其中选择题6个,判断题4个.甲、乙二人依次各抽一题.
(1)甲抽到选择题、乙抽到判断题的概率是多少?
(2)甲、乙二人中至少有一人抽到选择题的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}满足an+1+(﹣1)nan=2n﹣1,则{an}的前60项和为( )
A. 3690 B. 3660 C. 1845 D. 1830
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn,a1=1,Sn=2an+1,则Sn=( ).
A. 2n-1 B.
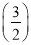 n-1 C.
n-1 C. 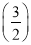 n-1 D.
n-1 D. 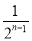
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为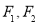 ,上、下顶点分别是
,上、下顶点分别是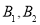 ,点
,点 是
是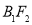 的中点,若
的中点,若 ,且
,且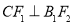 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过
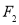 的直线
的直线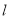 与椭圆
与椭圆 交于不同的两点
交于不同的两点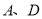 ,求
,求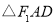 的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
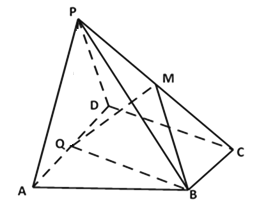
查看答案和解析>>【题目】如图,在四棱锥
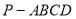 中,
中, 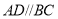 ,
, ,
,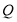 是
是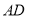 的中点,
的中点, 是棱
是棱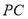 上的点,
上的点, ,
,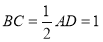 ,
, ,
, .
.
(1)求证:平面
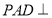 底面
底面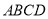 ;
;(2)设
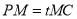 ,若二面角
,若二面角 的平面角的大小为
的平面角的大小为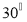 ,试确定
,试确定 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场对某一商品搞活动,已知该商品每一个的进价为3元,销售价为8元,每天售出的第20个及之后的半价出售.该商场统计了近10天的这种商品销量,如图所示:设
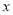 为每天商品的销量,
为每天商品的销量,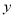 为该商场每天销售这种商品的的利润.从日利润不少于96元的几天里任选2天,则选出的这2天日利润都是97元的概率为( )
为该商场每天销售这种商品的的利润.从日利润不少于96元的几天里任选2天,则选出的这2天日利润都是97元的概率为( )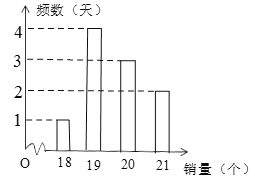
A.
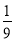 B.
B.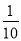 C.
C.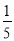 D.
D.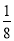
相关试题

