【题目】四棱锥P﹣ABCD中,PD⊥底面ABCD,AD∥BC,AC⊥DB,∠CAD=60°,AD=2,PD=1.
(1)证明:AC⊥BP;
(2)求二面角C﹣AP﹣D的平面角的余弦值.
参考答案:
【答案】
(1)
证明:∵PD⊥底面ABCD,AC平面ABCD;
∴AC⊥PD;
又AC⊥BD,BD∩PD=D;
∴AC⊥平面PBD,BP平面PBD;
∴AC⊥BP;
(2)
解:设AC∩BD=O,以O为坐标原点,OD,OA为x,y轴建立如图空间直角坐标系O﹣xyz,则:
O(0,0,0),D( ![]() ,0,0),A(0,1,0),P(
,0,0),A(0,1,0),P( ![]() ,0,1);
,0,1);
∴ ![]() ,
, ![]() ,
, ![]() ;
;
设平面ACP的法向量 ![]() ,平面ADP的法向量
,平面ADP的法向量 ![]() ;
;
由  得,
得, ![]() ,取x1=1,则
,取x1=1,则 ![]() ;
;
同理,由  得,
得, ![]() ;
;
∴  ;
;
∴二面角C﹣AP﹣D的平面角的余弦值为 ![]() .
.

【解析】(1)根据线面垂直的性质即可得到AC⊥PD,而由条件AC⊥BD,这样根据线面垂直的判定定理便可得出AC⊥平面PBD,进而便可证出AC⊥BP;(2)可设AC与BD交于点O,这样由条件便可分别以OD,OA为x轴,y轴,建立空间直角坐标系,从而可以求出点O,D,A,P四点的坐标,进而得出向量 ![]() 的坐标,可设平面ACP的法向量
的坐标,可设平面ACP的法向量 ![]() ,平面ADP的法向量
,平面ADP的法向量 ![]() ,这样根据
,这样根据  便可得出法向量
便可得出法向量 ![]() 的坐标,同理便可得出法向量
的坐标,同理便可得出法向量 ![]() 的坐标,从而便可求出
的坐标,从而便可求出 ![]() 的值,即得出二面角C﹣AP﹣D的平面角的余弦值.
的值,即得出二面角C﹣AP﹣D的平面角的余弦值.
【考点精析】通过灵活运用直线与平面垂直的性质,掌握垂直于同一个平面的两条直线平行即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】箱中有6张卡片,分别标有1,2,3,…,6。
(1)抽取一张记下号码后不放回,再抽取一张记下号码,求两次之和为偶数的概率;
(2)抽取一张记下号码后放回,再抽取一张记下号码,求两个号码中至少一个为偶数的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】双曲线
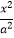 ﹣
﹣ 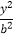 =1(a>0,b>0)的左、右焦点分别为F1 , F2 , P为双曲线上一点,且
=1(a>0,b>0)的左、右焦点分别为F1 , F2 , P为双曲线上一点,且 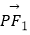
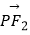 =0,△F1PF2的内切圆半径r=2a,则双曲线的离心率e= .
=0,△F1PF2的内切圆半径r=2a,则双曲线的离心率e= . -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC,满足bcosC+
 bsinC﹣a﹣c=0
bsinC﹣a﹣c=0
(1)求角B的值;
(2)若a=2,且AC边上的中线BD长为 ,求△ABC的面积.
,求△ABC的面积. -
科目: 来源: 题型:
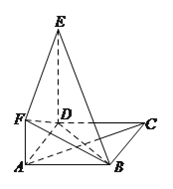
查看答案和解析>>【题目】如图所示,正方形
 与直角梯形
与直角梯形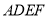 所在平面互相垂直,
所在平面互相垂直, 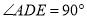 ,
, 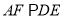 ,
, 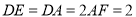 .
.
(I)求证:
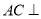 平面
平面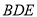 .
.(II)求证:
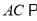 平面
平面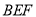 .
.(III)求四面体
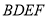 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线
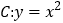 的焦点为F,动点P在直线
的焦点为F,动点P在直线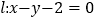 上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.(1)求△APB的重心G的轨迹方程.
(2)证明∠PFA=∠PFB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在(0,+∞)上的函数f(x)=a(x+
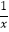 )﹣|x﹣
)﹣|x﹣ 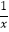 |(a∈R).
|(a∈R).
(1)当a= 时,求f(x)的单调区间;
时,求f(x)的单调区间;
(2)若f(x)≥ x对任意的x>0恒成立,求a的取值范围.
x对任意的x>0恒成立,求a的取值范围.
相关试题

