搜索
【题目】双曲线 
﹣ 
=1（a＞0，b＞0）的左、右焦点分别为F1 ， F2 ， P为双曲线上一点，且 
=0，△F1PF2的内切圆半径r=2a，则双曲线的离心率e= ．
参考答案：
【答案】5
【解析】解：可设P为第一象限的点，
由双曲线的定义可得|PF1|﹣|PF2|=2a，①
=0，可得PF1⊥PF2 ，
由勾股定理可得|PF1|2+|PF2|2=|F1F2|2=4c2 ， ②
②﹣①2 ， 可得2|PF1||PF2|=4c2﹣4a2=4b2 ，
即有|PF1|+|PF2|= 
，
由三角形的面积公式可得 
r（|PF1|+|PF2|+|F1F2|）= |PF1||PF2|，
即为2a（ +2c）=2b2 ，
即有c+2a= 
，两边平方可得
c2+4a2+4ac=c2+b2=c2+c2﹣a2 ，
即c2﹣4ac﹣5a2=0，解得c=5a（c=﹣a舍去），
即有e= 
=5．
所以答案是：5．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
的最小正周期是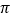
，且当
时，
取得最大值3.（1）求
的解析式及单调增区间；（2）若
，且
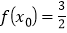，求
；（3）将函数
的图象向右平移
个单位长度后得到函数
的图象，且是偶函数，求m的最小值. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知实数x，y满足
，则目标函数2x+y的最大值为 ， 目标函数4x2+y2的最小值为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】箱中有6张卡片，分别标有1，2，3，…，6。
(1)抽取一张记下号码后不放回，再抽取一张记下号码，求两次之和为偶数的概率；
(2)抽取一张记下号码后放回，再抽取一张记下号码，求两个号码中至少一个为偶数的概率。
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC，满足bcosC+
bsinC﹣a﹣c=0
（1）求角B的值；
（2）若a=2，且AC边上的中线BD长为
，求△ABC的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】四棱锥P﹣ABCD中，PD⊥底面ABCD，AD∥BC，AC⊥DB，∠CAD=60°，AD=2，PD=1．
（1）证明：AC⊥BP；
（2）求二面角C﹣AP﹣D的平面角的余弦值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，正方形
与直角梯形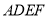
所在平面互相垂直， 
， 
， 
．
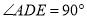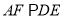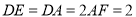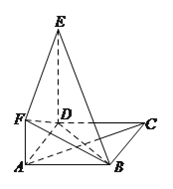
（I）求证：
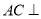平面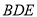
．（II）求证：
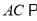平面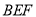
．（III）求四面体
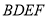的体积．
相关试题
