【题目】过抛物线C:y2=2px(p>0)的焦点F的直线交抛物线于A,B两点,且A,B两点的纵坐标之积为﹣4.
(1)求抛物线C的方程;
(2)已知点D的坐标为(4,0),若过D和B两点的直线交抛物线C的准线于P点,求证:直线AP与x轴交于一定点.
参考答案:
【答案】
(1)解:设A(x1,y1),B(x2,y2),
设直线AB的方程为x=my+ ![]()
与抛物线的方程联立 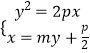 ,得y2﹣2mpy﹣p2=0,
,得y2﹣2mpy﹣p2=0,
∴y1y2=﹣p2=﹣4,
解得p=±2,
∵p>0,
∴p=2
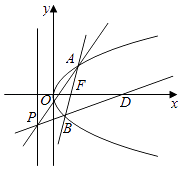
(2)解:依题意,直线BD与x轴不垂直,∴x2=4.
∴直线BD的方程可表示为,y= ![]() (x﹣4)①
(x﹣4)①
∵抛物线C的准线方程为,x=﹣1②
由①,②联立方程组可求得P的坐标为(﹣1,﹣ ![]() )
)
由(1)可得y1y2=﹣4,
∴P的坐标可化为(﹣1, ![]() ),
),
∴kAP= ![]() =
= ![]() ,
,
∴直线AP的方程为y﹣y1= ![]() (x﹣x1),
(x﹣x1),
令y=0,可得x=x1﹣ ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]()
∴直线AP与x轴交于定点( ![]() ,0).
,0).
【解析】(1)设A(x1 , y1),B(x2 , y2),设直线AB的方程为x=my+ ![]() ,联立方程组,根据A,B两点的纵坐标之积为﹣4,即可求出p的值,(2)表示出直线BD的方程可表示为,y=
,联立方程组,根据A,B两点的纵坐标之积为﹣4,即可求出p的值,(2)表示出直线BD的方程可表示为,y= ![]() (x﹣4)①,抛物线C的准线方程为,x=﹣1②,构成方程组,解得P的坐标,求出直线AP的斜率,得到直线AP的方程,求出交点坐标即可.
(x﹣4)①,抛物线C的准线方程为,x=﹣1②,构成方程组,解得P的坐标,求出直线AP的斜率,得到直线AP的方程,求出交点坐标即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
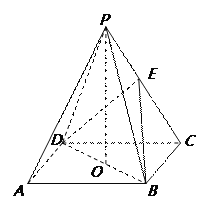
.求证:(Ⅰ)PA∥平面BDE;(Ⅱ)平面PAC⊥平面BDE;(III)若PB与底面所成的角为600, AB=2a,求三棱锥E-BCD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱柱ABC﹣A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AA1、A1B1上,且AE=
 ,A1F=
,A1F=  ,CE⊥EF.
,CE⊥EF.
(Ⅰ)证明:平面ABB1A1⊥平面ABC;
(Ⅱ)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求适合下列条件的圆锥曲线的标准方程:
(1)抛物线的焦点是椭圆
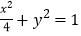 的上顶点;
的上顶点;(2)椭圆的焦距是8,离心率等于
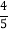 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某中学高中某学科竞赛中,该中学100名考生的参赛成绩统计如图所示.

(1)求这100名考生的竞赛平均成绩(同一组中数据用该组区间中点作代表);
(2)记70分以上为优秀,70分及以下为合格,结合频率分布直方图完成下表,并判断是否有99%的把握认为该学科竞赛成绩与性别有关?
合格
优秀
合计
男生
18
女生
25
合计
100
附:
 .
.
0.050
0.010
0.005

3.841
6.635
7.879
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点A(0,2)的直线
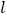 与椭圆C:
与椭圆C: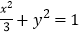 交于P,Q两点.
交于P,Q两点.(1)若直线
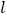 的斜率为k,求k的取值范围;
的斜率为k,求k的取值范围;(2)若以PQ为直径的圆经过点E(1,0),求直线
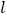 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体
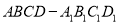 中,点
中,点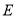 是棱
是棱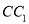 上的一个动点,平面
上的一个动点,平面 交棱
交棱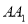 于点
于点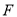 .给出下列命题:
.给出下列命题: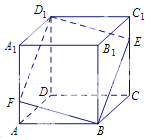
①存在点
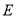 ,使得
,使得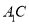 //平面
//平面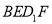 ;
;②对于任意的点
 ,平面
,平面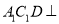 平面
平面 ;
;③存在点
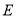 ,使得
,使得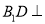 平面
平面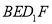 ;
;④对于任意的点
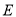 ,四棱锥
,四棱锥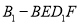 的体积均不变.
的体积均不变.其中正确命题的序号是______.(写出所有正确命题的序号).
相关试题

