【题目】已知数列{an}的前n项和为Sn , 且Sn= ![]() +
+ ![]() .
.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an+2﹣an+ ![]() ,且数列{bn}的前n项和为Tn , 求证:Tn<2n+
,且数列{bn}的前n项和为Tn , 求证:Tn<2n+ ![]() .
.
参考答案:
【答案】
(1)解:当n≥2时,
an=Sn﹣Sn﹣1
= ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]()
=n+1,
又n=1时,
a1=S1=2适合an=n+1,
∴an=n+1
(2)证明:由(1)知:
bn=n+3﹣(n+1)+ ![]()
=2+ ![]() ×(
×( ![]() ﹣
﹣ ![]() ),
),
∴Tn=b1+b2+b3+…+bn
=2n+ ![]() ×(
×( ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )
)
=2n+ ![]() ×(
×( ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )
)
<2n+ ![]() :
:
【解析】(1)根据数列的通项an和Sn的关系,即可求解数列{an}的通项公式;(2)由bn=2+ ![]() (
( ![]() ﹣
﹣ ![]() ),即可利用裂项相消求解数列的和,得以证明.
),即可利用裂项相消求解数列的和,得以证明.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系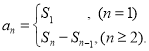 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017山西孝义考前热身】已知函数
 (
(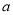 是常数),
是常数),(1)求函数
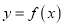 的单调区间;
的单调区间;(2)当
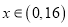 时,函数
时,函数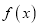 有零点,求
有零点,求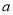 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足:a4=7,a10=19,其前n项和为Sn .
(1)求数列{an}的通项公式an及Sn;
(2)若等比数列{bn}的前n项和为Tn , 且b1=2,b4=S4 , 求Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】Sn为数列的前n项和,已知an>0,an2+2an=4Sn﹣1.
(1)求{an}的通项公式;
(2)求{an}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017河北唐山三模】已知函数
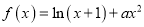 ,
, 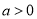 .
.(1)讨论函数
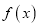 的单调性;
的单调性;(2)若函数
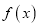 在区间
在区间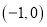 有唯一零点
有唯一零点 ,证明:
,证明: 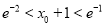 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017福建三明5月质检】已知函数
 ,
,  .
. (Ⅰ)当
 时,求证:过点
时,求证:过点 有三条直线与曲线
有三条直线与曲线 相切;
相切;(Ⅱ)当
 时,
时,  ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知bcos2
 +acos2
+acos2  =
=  c.
c.
(Ⅰ)求证:a,c,b成等差数列;
(Ⅱ)若C= ,△ABC的面积为2
,△ABC的面积为2 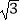 ,求c.
,求c.
相关试题

