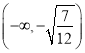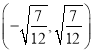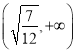【题目】【2017福建三明5月质检】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求证:过点
时,求证:过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切;
相切;
(Ⅱ)当![]() 时,
时, ![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(I)详见解析;(II)![]() .
.
【解析】
解法一:(Ⅰ)当![]() 时,
时, ![]() ,
,
![]()
![]()
设直线与曲线![]() 相切,其切点为
相切,其切点为![]() ,
,
则曲线![]() 在点
在点![]() 处的切线方程为:
处的切线方程为: ![]() ,
,
因为切线过点![]() ,所以
,所以![]() ,
,
即![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,
,
设![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
, ![]()
∴![]() 在三个区间
在三个区间![]() 上至少各有一个根
上至少各有一个根
又因为一元三次方程至多有三个根,所以方程![]() 恰有三个根,
恰有三个根,
故过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切.
相切.
(Ⅱ)∵当![]() 时,
时, ![]() ,即当
,即当![]() 时,
时, ![]()
∴当![]() 时,
时, ![]() ,
,
设![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() .
.
(1)当![]() 时,∵
时,∵![]() ,∴
,∴![]() ,从而
,从而![]() (当且仅当
(当且仅当![]() 时,等号成立)
时,等号成立)
∴![]() 在
在![]() 上单调递增,
上单调递增,
又∵![]() ,∴当
,∴当![]() 时,
时, ![]() ,从而当
,从而当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递减,又∵
上单调递减,又∵![]() ,
,
从而当![]() 时,
时, ![]() ,即
,即![]()
于是当![]() 时,
时, ![]() .
.
(2)当![]() 时,令
时,令![]() ,得
,得![]() ,∴
,∴![]() ,
,
故当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
又∵![]() ,∴当
,∴当![]() 时,
时, ![]() ,
,
从而当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递增,又∵
上单调递增,又∵![]() ,
,
从而当![]() 时,
时, ![]() ,即
,即![]()
于是当![]() 时,
时, ![]() ,
,
综合得![]() 的取值范围为
的取值范围为![]() .
.
解法二:(Ⅰ)当![]() 时,
时, ![]() ,
,
![]()
![]() ,
,
设直线与曲线![]() 相切,其切点为
相切,其切点为![]() ,
,
则曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
因为切线过点![]() ,所以
,所以![]() ,
,
即![]()
![]() ,
,
∵![]() ,∴
,∴![]()
设![]() ,则
,则![]() ,令
,令![]() 得
得![]()
当![]() 变化时,
变化时, ![]() ,
, ![]() 变化情况如下表:
变化情况如下表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| ↗ | 极大值
| ↘ | 极小值 | ↗ |
∴![]() 恰有三个根,
恰有三个根,
故过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切.
相切.
(Ⅱ)同解法一.
-
科目: 来源: 题型:
查看答案和解析>>【题目】Sn为数列的前n项和,已知an>0,an2+2an=4Sn﹣1.
(1)求{an}的通项公式;
(2)求{an}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 且Sn=
 +
+  .
.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an+2﹣an+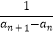 ,且数列{bn}的前n项和为Tn , 求证:Tn<2n+
,且数列{bn}的前n项和为Tn , 求证:Tn<2n+ 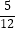 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017河北唐山三模】已知函数
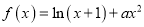 ,
, 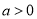 .
.(1)讨论函数
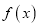 的单调性;
的单调性;(2)若函数
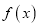 在区间
在区间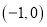 有唯一零点
有唯一零点 ,证明:
,证明: 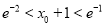 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知bcos2
 +acos2
+acos2  =
=  c.
c.
(Ⅰ)求证:a,c,b成等差数列;
(Ⅱ)若C= ,△ABC的面积为2
,△ABC的面积为2 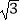 ,求c.
,求c. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,点M是AB的中点,则直线DB1与MC所成角的余弦值为( )
A.﹣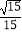
B.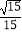
C.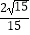
D.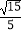
-
科目: 来源: 题型:
查看答案和解析>>【题目】双曲线
 =1(a>0,b>0)的左右焦点分别为F1 , F2渐近线分别为l1 , l2 , 位于第一象限的点P在l1上,若l2⊥PF1 , l2∥PF2 , 则双曲线的离心率是( )
=1(a>0,b>0)的左右焦点分别为F1 , F2渐近线分别为l1 , l2 , 位于第一象限的点P在l1上,若l2⊥PF1 , l2∥PF2 , 则双曲线的离心率是( )
A.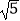
B.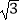
C.2
D.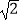
相关试题