

【题目】在平面直角坐标系中,已知曲线![]() (
(![]() 为参数),直线
为参数),直线![]() (
(![]() 为参数,
为参数, ![]() ),直线
),直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程及点
的极坐标方程及点![]() 的极坐标;
的极坐标;
(2)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于在
交于在![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;点
;点![]() 的极坐标为
的极坐标为![]() ;(2)16.
;(2)16.
【解析】
(1)直接利用消去参数法,将参数方程转化为直角坐标方程,再利用互化公式 ,将直角坐标方程转换为极坐标方程,即可求出曲线
,将直角坐标方程转换为极坐标方程,即可求出曲线![]() 和直线
和直线![]() 的极坐标方程,联立方程组,通过
的极坐标方程,联立方程组,通过![]() 求出
求出![]() ,从而可求出点
,从而可求出点![]() 的极坐标;
的极坐标;
(2)利用互化公式求出![]() 的极坐标方程,设
的极坐标方程,设![]() ,
,![]() ,将
,将![]() 代入
代入![]() 的极坐标方程,根据韦达定理求出
的极坐标方程,根据韦达定理求出![]() ,
,![]() ,进而求出
,进而求出![]() 和
和![]() ,从而可求出
,从而可求出![]() 的值.
的值.
解:(1)已知曲线![]() 为参数),
为参数),
消去参数![]() ,可得曲线
,可得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
将 代入得
代入得![]() 的极坐标方程为
的极坐标方程为![]() ,
,
由于直线![]() 为参数,
为参数,![]() ,
,
可得![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),
),
由于直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,
,
将![]() 代入曲线
代入曲线![]() ,得
,得![]() ,
,
则![]() ,得
,得![]() ,
,
又![]() ,所以
,所以![]() ,则
,则![]() ,
,
此时![]() ,所以点
,所以点![]() 的极坐标为
的极坐标为![]() .
.
(2)由于![]() 的直角坐标方程为
的直角坐标方程为![]() ,则圆心
,则圆心![]() ,
,
则![]() 的极坐标方程为:
的极坐标方程为:![]() ,
,
设![]() ,
,![]() ,
,
将![]() 代入
代入![]() 的极坐标方程
的极坐标方程![]() ,
,
得![]() ,
,![]() ,
,
所以![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
又因为![]() ,
,
![]() ,
,
所以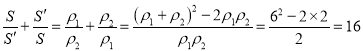 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立坐标系,曲线
轴正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .在平面直角坐标系
.在平面直角坐标系![]() 中,曲线
中,曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到定直线
到定直线![]() 的距离小1.
的距离小1.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .设线段
.设线段![]() ,
, ![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生活超市有一专柜预代理销售甲乙两家公司的一种可相互替代的日常生活用品.经过一段时间分别单独试销甲乙两家公司的商品,从销售数据中随机各抽取50天,统计每日的销售数量,得到如下的频数分布条形图.甲乙两家公司给该超市的日利润方案为:甲公司给超市每天基本费用为90元,另外每销售一件提成1元;乙公司给超市每天的基本费用为130元,每日销售数量不超过83件没有提成,超过83件的部分每件提成10元.
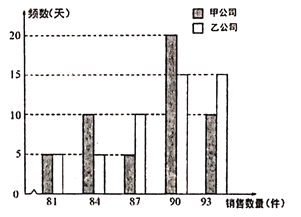
(Ⅰ)求乙公司给超市的日利润![]() (单位:元)与日销售数量
(单位:元)与日销售数量![]() 的函数关系;
的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
(1)求甲公司产品销售数量不超过87件的概率;
(2)如果仅从日均利润的角度考虑,请你利用所学过的统计学知识为超市作出抉择,选择哪家公司的产品进行销售?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将 2013 年编号为 1,2014 年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从 1 到 6 作为自变量进行回归分析),得到回归直线![]() ,其相关指数
,其相关指数![]() ,给出下列结论,其中正确的个数是( )
,给出下列结论,其中正确的个数是( )

①公共图书馆业机构数与年份的正相关性较强
②公共图书馆业机构数平均每年增加13.743个
③可预测 2019 年公共图书馆业机构数约为3192个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() :
:![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)若![]() ,求直线的方程;
,求直线的方程;
(2)过点![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,若线段
两点,若线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求点
,求点![]() 到直线
到直线![]() 与
与![]() 距离和的最大值.
距离和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
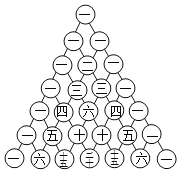
【题目】杨辉三角,又称帕斯卡三角,是二项式系数在三角形中的一种几何排列,在我国南宋数学家杨辉所著的《评解九章算法》(![]() 年)一书中用如图所示的三角形解释二项式乘方展开式的系数规律,现把杨辉三角中的数从上到下,从左到右依次排列,得数列:
年)一书中用如图所示的三角形解释二项式乘方展开式的系数规律,现把杨辉三角中的数从上到下,从左到右依次排列,得数列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …….记作数列
…….记作数列![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通安全法有规定:机动车行经人行横道时,应当减速行驶;遇行人正在通过人行横道,应当停车让行.机动车行经没有交通信号的道路时,遇行人横过马路,应当避让.我们将符合这条规定的称为“礼让斑马线”,不符合这条规定的称为“不礼让斑马线”.下表是六安市某十字路口监控设备所抓拍的5个月内驾驶员“不礼让斑马线”行为的统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
“不礼让斑马线”的驾驶员人数 | 120 | 105 | 100 | 85 | 90 |
(1)根据表中所给的5个月的数据,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)求“不礼让斑马线”的驾驶员人数![]() 关于月份
关于月份![]() 之间的线性回归方程;
之间的线性回归方程;
(3)若从4,5月份“不礼让斑马线”的驾驶员中分别选取4人和2人,再从所选取的6人中任意抽取2人进行交规调查,求抽取的2人分别来自两个月份的概率;
参考公式:线性回归方程![]() ,其中
,其中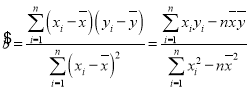 ,
,![]() ,
, .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com