【题目】(12分) 在△ABC中,a、b、c分别为角A、B、C的对边,且![]() ,
,
(1)求![]() 的度数;
的度数;
(2)若![]() ,
, ![]() ,求b和c的值.
,求b和c的值.
参考答案:
【答案】解:(1)由题设得2[1-cos(B+C)]-(2cos2A-1)=![]() ,
,
∵ cos(B+C)=-cosA,∴ 2(1+cosA)-2cos2A+1=![]() ,
,
整理得(2cosA-1)2=0,∴ cosA=![]() ,∴ A=60°.
,∴ A=60°.
(2)∵ cosA=![]() =
=![]() =
=![]() =
=![]()
∴![]() =
=![]() ,∴ bc=2. 又∵ b+c=3,∴ b=1, c=2或b=2, c=1.
,∴ bc=2. 又∵ b+c=3,∴ b=1, c=2或b=2, c=1.
【解析】试题分析:本试题主要是考查了解三角形中边角的转化,以及余弦定理的运用.(1)将已知的条件![]() ,利用倍角进行降幂,得到关于角
,利用倍角进行降幂,得到关于角![]() 的三角方程,从中求解方程即可;(2)由余弦定理得
的三角方程,从中求解方程即可;(2)由余弦定理得![]() ,将
,将![]() 代入,化简得
代入,化简得![]() ,最后联立方程
,最后联立方程![]() ,求解方程即可得到
,求解方程即可得到![]() 的值.
的值.
试题解析:(1)由条件![]() 得
得![]()
∴![]() 即
即![]() ,也就是
,也就是![]()
∴![]() ,∵
,∵![]() ,∴
,∴![]()
(2)由余弦定理得, ![]() 即
即![]() ,也就是
,也就是![]()
所以![]() ,又因为
,又因为![]() ,所以
,所以![]()
联立方程![]() ,解得
,解得![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项 ,
,  的部分项
的部分项 、
、 、 、
、 、 恰为等比数列,且
恰为等比数列,且 ,
, ,
, .
.(1)求数列
 的通项公式
的通项公式 (用
(用 表示);
表示);(2)设数列
 的前
的前 项和为
项和为 , 求证:
, 求证:  (
( 是正整数
是正整数 -
科目: 来源: 题型:
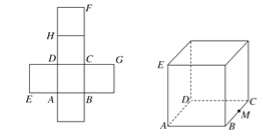
查看答案和解析>>【题目】【2017银川一中高考模拟文】一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N。
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH;
(3)过点M,N,H的平面将正方体分割为两部分,求这两部分的体积比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大学的
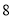 名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车.每车限坐
名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车.每车限坐 名同学(乘同一辆车的
名同学(乘同一辆车的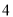 名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的
名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的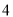 名同学中恰有
名同学中恰有 名同学是来自于同一年级的乘坐方式共有_______种(有数字作答).
名同学是来自于同一年级的乘坐方式共有_______种(有数字作答). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
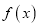 为定义在
为定义在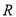 上的偶函数,当
上的偶函数,当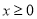 时,有
时,有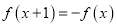 ,且当
,且当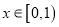 时,
时, 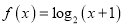 ,给出下列命题:
,给出下列命题:①
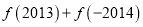 的值为
的值为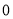 ;②函数
;②函数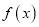 在定义域上为周期是2的周期函数;
在定义域上为周期是2的周期函数;③直线
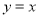 与函数
与函数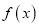 的图像有1个交点;④函数
的图像有1个交点;④函数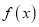 的值域为
的值域为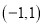 .
.其中正确的命题序号有__________ .
-
科目: 来源: 题型:
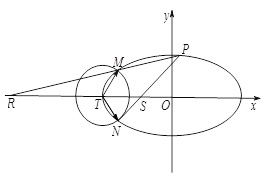
查看答案和解析>>【题目】如图,已知椭圆
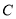 :
: 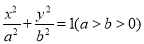 的离心率为
的离心率为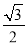 ,以椭圆
,以椭圆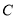 的左顶点
的左顶点 为圆心作圆
为圆心作圆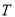 :
: 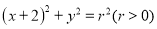 ,设圆
,设圆 与椭圆
与椭圆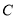 交于点
交于点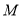 与点
与点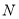 .
.
(1)求椭圆
 的方程;
的方程;(2)求
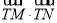 的最小值,并求此时圆
的最小值,并求此时圆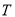 的方程;
的方程;(3)设点
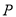 是椭圆
是椭圆 上异于
上异于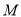 ,
, 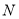 的任意一点,且直线
的任意一点,且直线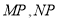 分别与
分别与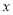 轴交于点
轴交于点 ,
, 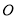 为坐标原点,求证:
为坐标原点,求证: 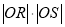 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“开门大吉”是中央电视台推出的娱乐节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌
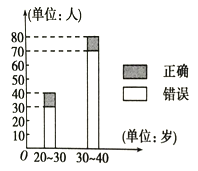
的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
(1) 完成下列2×2列联表(见答题纸);
(2)判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由.(下面的临界值表供参考)

0.10
0.05
0.010
0.005
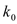
2.706
3.841
6.635
7.879
(参考公式:
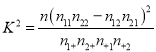 ,
, 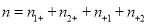 )
)
相关试题

