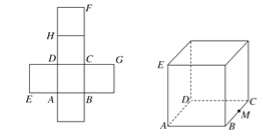
【题目】【2017银川一中高考模拟文】一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N。
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH;
(3)过点M,N,H的平面将正方体分割为两部分,求这两部分的体积比.
参考答案:
【答案】(1)详见解析;(2)详见解析. (3) 3∶1
【解析】 (1)点F,G,H的位置如图所示.

(2)证明:连接BD,设O为BD的中点,连接OM,OH,AC,BH,MN。
∵M,N分别是BC,GH的中点,
∴OM∥CD,且OM=![]() CD,NH∥CD,且NH=
CD,NH∥CD,且NH=![]() CD,
CD,
∴OM∥NH,OM=NH,则四边形MNHO是平行四边形,∴MN∥OH,
又∵MN平面BDH,OH平面BDH,∴MN∥平面BDH。
(3)由(2)知OM∥NH,OM=NH,连接GM,MH,过点M,N,H的平面就是平面GMH,它将正方体分割为两个同高的棱柱,高都是GH,底面分别是四边形BMGF和三角形MGC,
体积比等于底面积之比,即3∶1。
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ln x-ax(a∈R)(e=2.718 28…是自然对数的底数).
(1)判断f(x)的单调性;
(2)当f(x)<0在(0,+∞)上恒成立时,求a的取值范围;
(3)证明:当x∈(0,+∞)时,
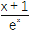 (1+x)
(1+x) 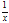 <e.
<e. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
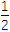 x2-2aln x+(a-2)x,a∈R.
x2-2aln x+(a-2)x,a∈R.(1)当a=1时,求函数f(x)的图象在点(1,f(1))处的切线方程.
(2)是否存在实数a,对任意的x1,x2∈(0,+∞)且x1≠x2有
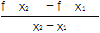 >a恒成立?若存在,求出a的取值范围;若不存在,说明理由.
>a恒成立?若存在,求出a的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项 ,
,  的部分项
的部分项 、
、 、 、
、 、 恰为等比数列,且
恰为等比数列,且 ,
, ,
, .
.(1)求数列
 的通项公式
的通项公式 (用
(用 表示);
表示);(2)设数列
 的前
的前 项和为
项和为 , 求证:
, 求证:  (
( 是正整数
是正整数 -
科目: 来源: 题型:
查看答案和解析>>【题目】某大学的
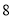 名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车.每车限坐
名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车.每车限坐 名同学(乘同一辆车的
名同学(乘同一辆车的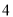 名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的
名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的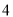 名同学中恰有
名同学中恰有 名同学是来自于同一年级的乘坐方式共有_______种(有数字作答).
名同学是来自于同一年级的乘坐方式共有_______种(有数字作答). -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分) 在△ABC中,a、b、c分别为角A、B、C的对边,且
 ,
,(1)求
 的度数;
的度数;(2)若
 ,
,  ,求b和c的值.
,求b和c的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
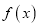 为定义在
为定义在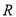 上的偶函数,当
上的偶函数,当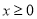 时,有
时,有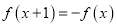 ,且当
,且当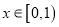 时,
时, 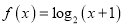 ,给出下列命题:
,给出下列命题:①
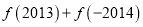 的值为
的值为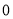 ;②函数
;②函数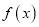 在定义域上为周期是2的周期函数;
在定义域上为周期是2的周期函数;③直线
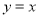 与函数
与函数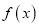 的图像有1个交点;④函数
的图像有1个交点;④函数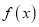 的值域为
的值域为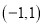 .
.其中正确的命题序号有__________ .
相关试题

