【题目】为了实现绿色发展,避免浪费能源,耨市政府计划对居民用电采用阶梯收费的方法.为此,相关部门在该市随机调查了20户居民六月份的用电量(单位:![]() )和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
)和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
用电量数据如下:18,63,72,82,93,98,106,110,118,130,134,139,147,163,180,194,212,237,260,324.
对应的家庭收入数据如下:0.21,0.24,0.35,0.40,0.52,0.60,0.58,0.65,0.65,0.63,0.68,0.80,0.83,0.93,0.97,0.96,1.1,1.2,1.5,1.8.
(1)根据国家发改委的指示精神,该市计划实施3阶阶梯电价,使75%的用户在第一档,电价为0.56元/![]() ;
;![]() 的用户在第二档,电价为0.61元/
的用户在第二档,电价为0.61元/![]() ;
;![]() 的用户在第三档,电价为0.86元/
的用户在第三档,电价为0.86元/![]() ;试求出居民用电费用
;试求出居民用电费用![]() 与用电量
与用电量![]() 间的函数关系式;
间的函数关系式;
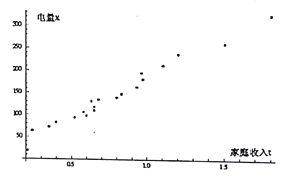
(2)以家庭收入![]() 为横坐标,电量
为横坐标,电量![]() 为纵坐标作出散点图(如图),求
为纵坐标作出散点图(如图),求![]() 关于
关于![]() 的回归直线方程(回归直线方程的系数四舍五入保留整数)
的回归直线方程(回归直线方程的系数四舍五入保留整数)![]() ;
;
(3)小明家的月收入7000元,按上述关系,估计小明家月支出电费多少元?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:一组相关数据![]() 的回归直线方程
的回归直线方程![]() 的斜率和截距的最小二乘法估计分别为.
的斜率和截距的最小二乘法估计分别为.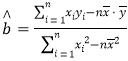 ,
,![]() ,其中
,其中![]() 为样本均值.
为样本均值.
参考答案:
【答案】(1) ;(2)
;(2)![]() ;(3)72.8.
;(3)72.8.
【解析】分析:(1)因为![]() ,
,
所以从用电量数据中得到第一档的临界值为第15个样本,即180,
第二档的临界值为第19个样本,即260.由此,可求居民用电费用![]() 与用电量
与用电量![]() 间的函数关系式;
间的函数关系式;
(2)计算可得![]() ,
,![]() ,代入公式可求
,代入公式可求![]() 关于
关于![]() 的回归直线方程
的回归直线方程
(3)把![]() 代入回归直线方程求出
代入回归直线方程求出![]() ,再把
,再把![]() 代入(1)函数解析式即可.
代入(1)函数解析式即可.
![]() ,所以,小明家月支出电费72.8元.
,所以,小明家月支出电费72.8元.
详解:(1)因为![]() ,
,
所以从用电量数据中得到第一档的临界值为第15个样本,即180,
第二档的临界值为第19个样本,即260.因此,
所以,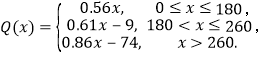
(2)由于![]() ,
,
![]() ,
,
 ,
,
所以![]() ,
,
从而回归直线方程为![]() .
.
(3)当![]() 时,
时,![]() ,
,
![]() ,所以,小明家月支出电费72.8元.
,所以,小明家月支出电费72.8元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正数数列
 的前
的前 项和为
项和为 ,且满足
,且满足 ;在数列
;在数列 中,
中,
(1)求数列
 和
和 的通项公式;
的通项公式;(2)设
 ,数列
,数列 的前
的前 项和为
项和为 . 若对任意
. 若对任意 ,存在实数
,存在实数 ,使
,使 恒成立,求
恒成立,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团
未参加书法社团
参加演讲社团
8
5
未参加书法社团
2
30
(1)从该班随机选 1 名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 8 名同学中,有 5 名男同学
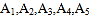 ,3名女同学
,3名女同学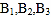 .现从这 5 名男同学和 3 名女同学中各随机选 1 人,求
.现从这 5 名男同学和 3 名女同学中各随机选 1 人,求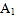 被选中且
被选中且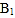 未被选中的概率.
未被选中的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
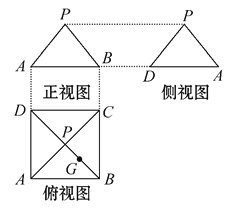
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥
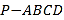 中,四边形
中,四边形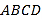 为矩形,
为矩形, 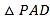 为等腰三角形,
为等腰三角形, 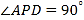 ,平面
,平面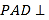 平面
平面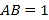 ,且
,且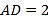 ,
, 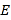 ,
, 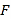 分别为
分别为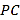 的中点.
的中点.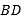
(1)证明:
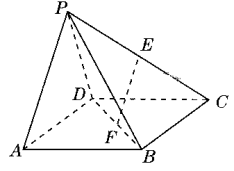 平面
平面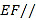 ;
;(2)证明:平面
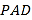 平面
平面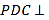 ;
;(3)求四棱锥
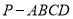 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数f(x)=4sin(2x+
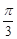 ), (x∈R)有下列命题:
), (x∈R)有下列命题:①y=f(x)是以2π为最小正周期的周期函数;
② y=f(x)可改写为y=4cos(2x-
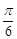 );
);③y=f(x)的图象关于(-
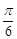 ,0)对称;
,0)对称;④ y=f(x)的图象关于直线x=-
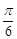 对称;
对称;其中正确的序号为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列
 中,
中, ,前
,前 项和
项和 满足条件
满足条件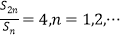 ,
,(1)求数列
 的通项公式和
的通项公式和 ;
;(2)记
 ,求数列
,求数列 的前
的前 项和
项和 .
.
相关试题

