搜索
【题目】如图所示，O是正六边形ABCDEF的中心，且
＝
，
＝
，
＝
.
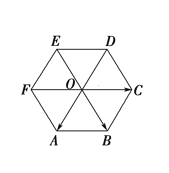
（1）与的长度相等、方向相反的向量有哪些？
（2）与共线的向量有哪些？
（3）请一一列出与，，.相等的向量．
参考答案：
【答案】（1）
，
，
，
.（2）
，，，，
，
，，
，
.
（3）与
相等的向量有，，；与
相等的向量有
，
，
；与
相等的向量有
，
，
.
【解析】
（1）根据正六边形的性质，图形中各线段长度都相等，只要方向相反即可.
（2）根据共线向量定理求解.
（3）根据相等的向量的定义求解.
（1）因为正六边形中各线段长度都相等，且方向相反的有：，，， .（2）由共线向量定理得：，，，，，，，，.与共线.
（3）由相等向量的定义得：与 相等的向量有，，；与 相等的向量有，，；与 相等的向量有，，.
-
科目： 来源： 题型：
查看答案和解析>>【题目】一组数据中的每一个数据都乘以2，再减去80，得到一组新数据，若求得新的数据的平均数是1.2，方差是4.4，则原来数据的平均数和方差分别是（ ）
A.40.6，1.1B.48.8，4.4C.81.2，44.4D.78.8，75.6
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知
是等差数列，满足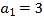
， 
，数列
满足
， 
，且
是等比数列.（1）求数列
和
的通项公式；（2）求数列
的前
项和. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行六面体ABCD－A1B1C1D1中，AA1⊥平面ABCD，且AB＝AD＝2，AA1＝
，∠BAD＝120°.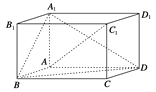
(1)求异面直线A1B与AC1所成角的余弦值；
(2)求二面角B－A1D－A的正弦值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】高中生在被问及“家，朋友聚集的地方，个人空间”三个场所中“感到最幸福的场所在哪里？”这个问题时，从中国某城市的高中生中，随机抽取了55人，从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是：选择家的占
、朋友聚集的地方占
、个人空间占.美国高中生答题情况是：朋友聚集的地方占
、家占
、个人空间占.如下表：在家里最幸福
在其它场所幸福
合计
中国高中生
美国高中生
合计
（Ⅰ）请将
列联表补充完整；试判断能否有
的把握认为“恋家”与否与国别有关；（Ⅱ）从被调查的不“恋家”的美国学生中，用分层抽样的方法选出4人接受进一步调查，再从4人中随机抽取2人到中国交流学习，求2人中含有在“个人空间”感到幸福的学生的概率.
附：
，其中
.
0.050
0.025
0.010
0.001
3.841
5.024
6.635
10.828
-
科目： 来源： 题型：
查看答案和解析>>【题目】 某工厂甲、乙两个车间包装同一种产品，在自动包装传送带上，每隔30分钟抽一包产品，称其重量是否合格，分别记录抽查数据如下(单位：千克)：
甲车间：102，101，99，98，103，98，99.
乙车间：110，115，90，85，75，115，110.
（1）这种抽样方式是何种抽样方法；
（2）试根据这组数据说明哪个车间产品较稳定？
-
科目： 来源： 题型：
查看答案和解析>>【题目】我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟定一个合理的月用水量标准x(吨)，一位居民的月用水量不超过x的部分按平价收费，超出x的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量(单位：吨)，将数据按照
，
，…，
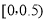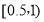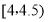分成9组，制成了如图所示的频率分布直方图.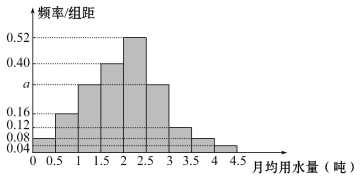
（1）求直方图中a的值.
（2）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由.
（3）若该市政府希望使85%的居民每月的用水量不超过标准x(吨)，估计x的值，并说明理由.
相关试题
