【题目】(12分)
在直角坐标系xOy中,曲线y=x2+mx–2与x轴交于A,B两点,点C的坐标为(0,1).当m变化时,解答下列问题:
(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.
参考答案:
【答案】(1)不会;(2)详见解析
【解析】(1)设![]() ,则
,则![]() 是方程
是方程![]() 的根,
的根,
所以![]() ,
,
则![]() ,
,
所以不会能否出现AC⊥BC的情况。
(2)解法1:过A,B,C三点的圆的圆心必在线段AB垂直平分线上,设圆心![]() ,则
,则![]() ,由
,由![]() 得
得![]() ,化简得
,化简得![]() ,所以圆E的方程为
,所以圆E的方程为![]() ,
,
令![]() 得
得![]() ,所以过A,B,C三点的圆在y轴上截得的弦长为
,所以过A,B,C三点的圆在y轴上截得的弦长为![]() ,所以
,所以
所以过A,B,C三点的圆在y轴上截得的弦长为定值
解法2:设过A,B,C三点的圆与y轴的另一个交点为D,
由![]() 可知原点O在圆内,由相交弦定理可得
可知原点O在圆内,由相交弦定理可得![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以过A,B,C三点的圆在y轴上截得的弦长为![]() ,为定值.
,为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形, 且∠DAB=90°,∠ABC=45°,CB=
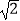 ,AB=2,PA=1
,AB=2,PA=1
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥C﹣MAD的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥P﹣ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形.
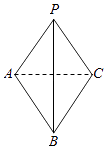
(1)证明:AB⊥PC;
(2)若AB=2PC=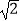 ,求三棱锥P﹣ABC的体积.
,求三棱锥P﹣ABC的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AB=4,EC∥FD,FD⊥底面ABCD,M是AB的中点.

(1)求证:平面CFM⊥平面BDF;
(2)若点N为线段CE的中点,EC=2,FD=3,求证:MN∥平面BEF. -
科目: 来源: 题型:
查看答案和解析>>【题目】电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
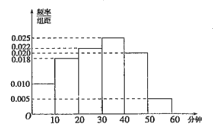
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
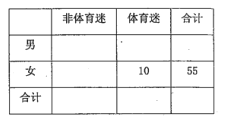
(1)根据已知条件完成上面的
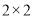 列联表,若按
列联表,若按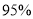 的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为
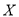 .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求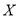 分布列,期望
分布列,期望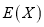 和方差
和方差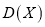 .
.附:
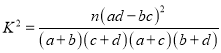

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:
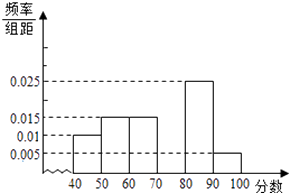
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.

(1)求n的值;
(2)把在前排就坐的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率.
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
相关试题

