【题目】如图,已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形, 且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1
,AB=2,PA=1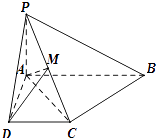
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥C﹣MAD的体积.
参考答案:
【答案】
(1)∵底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,
∴AB∥CD,
又AB平面PCD,CD平面PCD,
∴AB∥平面PCD
(2)∵∠ABC=45°,CB= ![]() ,AB=2,
,AB=2,
∴AC2=AB2+BC2﹣2ABBCcos45°= ![]() =2.
=2.
则AC2+BC2=AB2,∴BC⊥AC.
∵PA⊥平面ABCD,BC平面ABCD,∴PA⊥BC.
又PA∩AC=A,∴BC⊥平面PAC
(3)在直角梯形ABCD中,过C作CE⊥AB于点E,
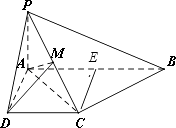
则四边形ADCE为矩形,∴AE=DC,AD=EC.
在Rt△CEB中,可得BE=BCcos45°= ![]() ,
,
CE=BCsin45°= ![]() ,∴AE=AB﹣BE=2﹣1=1
,∴AE=AB﹣BE=2﹣1=1
∴S△ADC= ![]() =
= ![]() =
= ![]() .,
.,
∵M是PC的中点,∴M到平面ADC的距离是P到平面ADC距离的一半,
∴VC﹣MAD=VM﹣ACD= ![]() ×S△ACD×(
×S△ACD×( ![]() PA)=
PA)= ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
【解析】(1)利用线面平行的判定定理证明;(2)利用勾股定理证明BC⊥AC,由PA⊥平面ABCD,可得PA⊥BC.从而可证得BC⊥平面PAC:(3)在直角梯形ABCD中,过C作CE⊥AB于点E,则四边形ADCE为矩形,AE=DC,AD=EC.求得CE,计算△ACD的面积,根据M到平面ADC的距离是P到平面ADC距离的一半,求得棱锥的高,代入体积公式计算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)
某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温
[10,15)
[15,20)
[20,25)
[25,30)
[30,35)
[35,40)
天数
2
16
36
25
7
4
以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.学#科@网
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个四棱锥底面为正方形,顶点在底面的射影为正方形的中心,且该四棱锥的体积为9,当其外接球表面积最小时,它的高为( )
A.3
B.2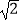
C.2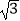
D.3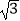
-
科目: 来源: 题型:
查看答案和解析>>【题目】在物理实验中,为了研究所挂物体的重量x对弹簧长度y的影响.某学生通过实验测量得到物体的重量与弹簧长度的对比表:
物体重量(单位g)
1
2
3
4
5
弹簧长度(单位cm)
1.5
3
4
5
6.5
参考公式:
①.样本数据x1 , x2 , …xn的标准差
s=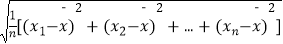 ,其中
,其中 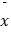 为样本的平均数;
为样本的平均数;
②.线性回归方程系数公式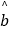 =
= 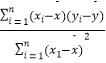 =
= 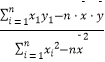 ,
, 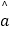 =
= 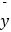 ﹣
﹣ 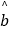
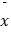 .
.
(1)画出散点图;
(2)利用所给的参考公式,求y对x的回归直线方程;
(3)预测所挂物体重量为8g时的弹簧长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥P﹣ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形.
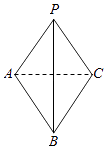
(1)证明:AB⊥PC;
(2)若AB=2PC=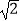 ,求三棱锥P﹣ABC的体积.
,求三棱锥P﹣ABC的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AB=4,EC∥FD,FD⊥底面ABCD,M是AB的中点.

(1)求证:平面CFM⊥平面BDF;
(2)若点N为线段CE的中点,EC=2,FD=3,求证:MN∥平面BEF. -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)
在直角坐标系xOy中,曲线y=x2+mx–2与x轴交于A,B两点,点C的坐标为(0,1).当m变化时,解答下列问题:
(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.
相关试题

