【题目】如图,三棱柱![]() 中,侧棱
中,侧棱![]() 平面
平面![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,且
,且![]() 分别是
分别是![]() 的中点.
的中点.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求锐二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]() ;
;
【解析】
试题分析:(1)要证明![]() 平面
平面![]() ,需证明
,需证明![]() 及
及![]() ,前面在平面中证明,利用勾股定理,即通过计算设
,前面在平面中证明,利用勾股定理,即通过计算设![]() ,则
,则![]() .∴
.∴![]() ,∴
,∴![]() .后者通过线面垂直与线线垂直的转化得,即由面
.后者通过线面垂直与线线垂直的转化得,即由面![]() 面
面![]() ,得
,得![]() 面
面![]() ,再得
,再得![]() 。(2)求二面角的余弦值,可通过作、证、算,本题可过
。(2)求二面角的余弦值,可通过作、证、算,本题可过![]() 作
作![]() ,则
,则![]() 为所求二面角的平面角.也可利用空间向量求,先建系,求出平面
为所求二面角的平面角.也可利用空间向量求,先建系,求出平面![]() 及平面
及平面![]() 的法向量,利用向量数量积求出两法向量的夹角,最后根据二面角与向量夹角关系得出结论.
的法向量,利用向量数量积求出两法向量的夹角,最后根据二面角与向量夹角关系得出结论.
试题解析:(1)连结![]() ,∵
,∵![]() 是等腰直角三角形
是等腰直角三角形![]() 斜边
斜边![]() 的中点,∴
的中点,∴![]() .
.
又![]() 三棱柱
三棱柱![]() 为直三棱柱,
为直三棱柱,
∴面![]() 面
面![]() ,
,
∴![]() 面
面![]() ,
,![]() . 2分
. 2分
设![]() ,则
,则![]() .
.
∴![]() ,∴
,∴![]() . 4分
. 4分
又![]() ,∴
,∴![]() 平面
平面![]() . 6分
. 6分
(2)以![]() 为坐标原点,
为坐标原点,![]() 分别为
分别为![]() 轴建立直角坐标系如图,设
轴建立直角坐标系如图,设![]() ,
,
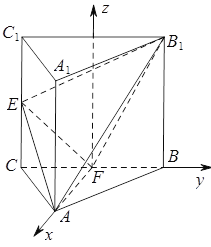
则![]() ,
,
![]() ,
,![]() . 8分
. 8分
由(1)知,![]() 平面
平面![]() ,
,
∴可取平面![]() 的法向量
的法向量![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由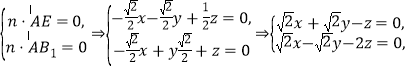
∴可取![]() . 10分
. 10分
设锐二面角![]() 的大小为
的大小为![]() ,
,
则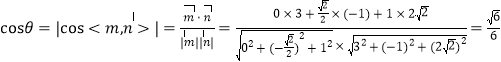 .
.
∴所求锐二面角![]() 的余弦值为
的余弦值为![]() . 12分
. 12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品原来每件售价为25元,年销售量8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到
 元.公司拟投入
元.公司拟投入 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入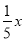 万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(wx+φ)(w>0,0<φ<π)的周期为π,图象的一个对称中心为(
 ,0),将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
,0),将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个  单位长度后得到函数g(x)的图象.
单位长度后得到函数g(x)的图象.
(1)求函数f(x)与g(x)的解析式
(2)是否存在x0∈( ),使得f(x0),g(x0),f(x0)g(x0)按照某种顺序成等差数列?若存在,请确定x0的个数,若不存在,说明理由;
),使得f(x0),g(x0),f(x0)g(x0)按照某种顺序成等差数列?若存在,请确定x0的个数,若不存在,说明理由;
(3)求实数a与正整数n,使得F(x)=f(x)+ag(x)在(0,nπ)内恰有2013个零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】对某种书籍每册的成本费
 (元)与印刷册数
(元)与印刷册数 (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.


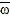




4.83
4.22
0.3775
60.17
0.60
-39.38
4.8
表中
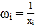 ,
,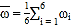 .
.为了预测印刷20千册时每册的成本费,建立了两个回归模型:
 ,
, .
.(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中选择的模型,求
 关于
关于 的回归方程,并预测印刷20千册时每册的成本费.
的回归方程,并预测印刷20千册时每册的成本费.附:对于一组数据
 ,
, ,…,
,…, ,其回归方程
,其回归方程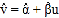 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为
 、
、 、
、 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).

(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次函数
 .
.(1)写出该函数的顶点坐标;
(2)如果该函数在区间
 上的最小值为
上的最小值为 ,求实数
,求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
已知
 ,函数
,函数 .
.(I)当
 为何值时,
为何值时, 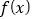 取得最大值?证明你的结论;
取得最大值?证明你的结论;(II) 设
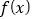 在
在 上是单调函数,求
上是单调函数,求 的取值范围;
的取值范围;(III)设
 ,当
,当 时,
时,  恒成立,求
恒成立,求 的取值范围.
的取值范围.
相关试题

