【题目】中学生研学旅行是通过集体旅行、集中食宿方式开展的研究性学习和旅行体验相结合的校外教育活动,是学校教育和校外教育衔接的创新形式,是综合实践育人的有效途径.每年暑期都会有大量中学生参加研学旅行活动.为了解某地区中学生暑期研学旅行支出情况,在该地区各个中学随机抽取了部分中学生进行问卷调查,从中统计得到中学生暑期研学旅行支出(单位:百元)频率分布直方图如图所示.

(1)利用分层抽样在![]() ,
,![]() ,
,![]() 三组中抽取5人,应从这三组中各抽取几人?
三组中抽取5人,应从这三组中各抽取几人?
(2)从(1)抽取的5人中随机选出2人,对其消费情况进行进一步分析,求这2人不在同一组的概率;
(3)假设同组中的每个数据都用该区间的左端点值代替,估计该地区中学生暑期研学旅行支出的平均值.
参考答案:
【答案】(1)从这三组中抽取的人数分别为3,1,1(2)![]() (3)
(3)![]() 百元
百元
【解析】
(1)利用分层抽样和频率分布直方图先求出再各区间的比例,再求出人数;
(2)先求出基本事件的总数,再求出这2人不在同一组的基本事件数,再求概率即可;
(3)由频率分布直方图的性质和平均数的计算公式即可求解.
(1)由频率分布直方图可知![]() ,
,![]() ,
,![]() 三组的频数的比为
三组的频数的比为
![]() ,
,
所以从![]() 中抽取:
中抽取:![]() 人,
人,
从![]() 中抽取:
中抽取:![]() 人,
人,
从![]() 中抽取:
中抽取:![]() 人,
人,
所以从这三组中抽取的人数分别为3,1,1;
(2)记![]() 中的3人为
中的3人为![]() ,
,![]() ,
,![]() ,
,![]() 中的1人为b,
中的1人为b,![]() 中的1人为c,
中的1人为c,
从这5人中随机选出2人,则样本空间
![]() 含
含![]() 个样本点,
个样本点,
设事件A:选出的2人不在同一组,
则![]() 含7个样本点,
含7个样本点,
所以![]() ;
;
(3)![]() ,
,
估计该地区中学生暑期研学旅行支出的平均值为![]() 百元.
百元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)满足f(x+1)-f(x)=-2x+1,且f(2)=15.
(1)求函数f(x)的解析式;
(2) 令g(x)=(2-2m)x-f(x).
① 若函数g(x)在x∈[0,2]上是单调函数,求实数m的取值范围;
② 求函数g(x)在x∈[0,2]上的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)讨论
 的单调性;
的单调性;(2)若
 ,直线
,直线 与曲线
与曲线 和曲线
和曲线 都相切,切点分别为
都相切,切点分别为 ,
, ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
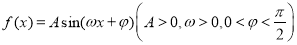 的部分图象如图所示,则下列叙述正确的是( )
的部分图象如图所示,则下列叙述正确的是( )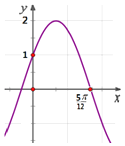
A.函数
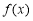 的图象可由
的图象可由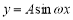 的图象向左平移
的图象向左平移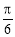 个单位得到
个单位得到B.函数
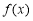 的图象关于直线
的图象关于直线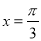 对称
对称C.函数
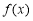 在区间
在区间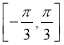 上是单调递增的
上是单调递增的D.函数
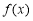 图象的对称中心为
图象的对称中心为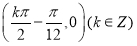
-
科目: 来源: 题型:
查看答案和解析>>【题目】在棱长均为
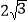 的四面体
的四面体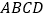 中,点
中,点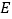 为
为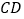 的中点,点
的中点,点 为
为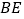 的中点.若点
的中点.若点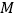 ,
,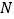 是平面
是平面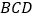 内的两动点,且
内的两动点,且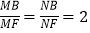 ,
,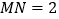 ,则
,则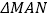 的面积为( )
的面积为( )A.
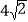 B. 3
B. 3C.
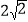 D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】“中国大能手”是央视推出的一档大型职业技能挑战赛类节目,旨在通过该节目,在全社会传播和弘扬“劳动光荣、技能宝贵、创造伟大”的时代风尚.某公司准备派出选手代表公司参加“中国大能手”职业技能挑战赛.经过层层选拔,最后集中在甲、乙两位选手在一项关键技能的区分上,选手完成该项挑战的时间越少越好.已知这两位选手在15次挑战训练中,完成该项关键技能挑战所用的时间(单位:秒)及挑战失败(用“×”表示)的情况如下表1:
序号

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
甲
×
96
93
×
92
×
90
86
×
×
83
80
78
77
75
乙
×
95
×
93
×
92
×
88
83
×
82
80
80
74
73
据表1中甲、乙两选手完成该项关键技能挑战成功所用时间的数据,应用统计软件得下表2:
数字特征
均值(单位:秒)方差
方差
甲
85
50.2
乙
84
54
(1)在表1中,从选手甲完成挑战用时低于90秒的成绩中,任取2个,求这2个成绩都低于80秒的概率;
(2)若该公司只有一个参赛名额,以该关键技能挑战成绩为标准,根据以上信息,判断哪位选手代表公司参加职业技能挑战赛更合适?请说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面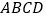 是平行四边形,
是平行四边形, 平面
平面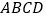 ,
, ,
, ,
,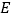 是棱
是棱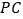 上的一点.
上的一点.(1)证明:
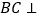 平面
平面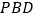 ;
; (2)若
 平面
平面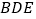 ,求
,求 的值;
的值;(3)在(2)的条件下,三棱锥
 的体积是18,求
的体积是18,求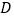 点到平面
点到平面 的距离.
的距离.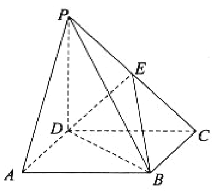
相关试题

