【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 都相切,切点分别为
都相切,切点分别为![]() ,
,![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1)分类讨论,详见解析;(2)详见解析.
【解析】
(1)首先写出函数![]() 定义域为
定义域为![]() ,求得
,求得![]() ,对
,对![]() 的范围进行讨论,从而确定出
的范围进行讨论,从而确定出![]() 的符号,确定出函数
的符号,确定出函数![]() 的单调性;
的单调性;
(2)可以从两个角度去分析,方法一是根据导数的几何意义,写出直线![]() 的方程为
的方程为![]() ,即
,即![]() ,也可以写成
,也可以写成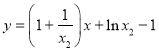 ,根据两条直线是同一条直线,得到
,根据两条直线是同一条直线,得到![]() ,且
,且![]() ,对式子进行整理可以得到
,对式子进行整理可以得到![]() ,构造函数
,构造函数![]() ,利用导数研究该函数的单调性及最值,从而可以证得结果;方法二是根据两条切线的斜率想的得到
,利用导数研究该函数的单调性及最值,从而可以证得结果;方法二是根据两条切线的斜率想的得到 ,进一步可以得到
,进一步可以得到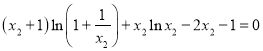 ,构造函数
,构造函数![]() ,利用导数研究该函数的单调性及最值得到结果.
,利用导数研究该函数的单调性及最值得到结果.
(1)![]() 定义域为
定义域为![]() ,
,
因为![]() ,
,
若![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
若![]() ,则当
,则当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)证法一:
证明:对于曲线![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
即![]() ,即
,即![]() ①.
①.
对于曲线![]() ,因为
,因为![]() ,所以
,所以![]()
所以![]() ,
,
直线![]() 的方程为
的方程为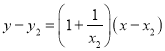 ,
,
即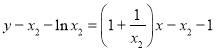 ,即
,即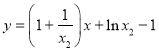 ②.
②.
因为①与②表示同一条直线,所以![]() ③,
③,
且![]() ④,
④,
④÷③,得![]() ,
,
所以![]() .
.
令![]() ,
,
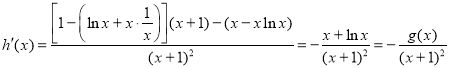 ,
,
由(1)知,![]() 在
在![]() 单调递增又
单调递增又![]()
![]() ∴
∴![]()
![]() 有唯一零点
有唯一零点![]() ,
,
且当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
所以![]() ,
,
又![]() ,即
,即![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() .
.
证法二:
证明:因为![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以直线![]() 的斜率为
的斜率为![]() ,
,
所以![]() ,所以
,所以 ,
,
又因为 ,
,
所以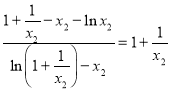 ,
,
所以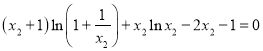 ,
,
令![]() ,
,
所以![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
又因为![]() ,
,![]() ,
,
所以存在![]() ,使得
,使得![]() ,
,
且当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
因为![]() ,所以
,所以![]() 在
在![]() 递减,
递减,
所以当![]() 时,
时, ,
,
所以![]() 在
在![]() 内无零点,
内无零点,
因为![]() 是
是![]() 的零点且
的零点且![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 年
年 月以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病例,均诊断为病毒性肺炎肺部感染,后被命名为新型冠状病毒肺炎(CoronaVirusDisease2019,COVID-19),简称“新冠肺炎”,下图是
月以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病例,均诊断为病毒性肺炎肺部感染,后被命名为新型冠状病毒肺炎(CoronaVirusDisease2019,COVID-19),简称“新冠肺炎”,下图是 年
年 月
月 日至
日至 月
月 日累计确诊人数随时间变化的散点图.
日累计确诊人数随时间变化的散点图.
为了预测在未采取强力措施下,后期的累计确诊人数,建立了累计确诊人数
 与时间变量
与时间变量 的两个回归模型,根据
的两个回归模型,根据 月
月 日至
日至 月
月 日的数据(时间变量
日的数据(时间变量 的值依次
的值依次 ,
, ,…,
,…, )建立模型
)建立模型 和
和 .
.参考数据:其中
 ,
, .
.






















(1)根据散点图判断,
 和
和 哪一个适宜作为累计确诊人数
哪一个适宜作为累计确诊人数 与时间变量
与时间变量 的回归方程类型?(给出判断即可,不必说明理由);
的回归方程类型?(给出判断即可,不必说明理由);(2)根据(1)的判断结果及附表中数据,建立
 关于
关于 的回归方程;
的回归方程;(3)以下是
 月
月 日至
日至 月
月 日累计确诊人数的真实数据,根据(2)的结果回答下列问题:
日累计确诊人数的真实数据,根据(2)的结果回答下列问题:时间
 月
月 日
日 月
月 日
日 月
月 日
日 月
月 日
日 月
月 日
日累计确诊人数的真实数据




(i)当
 月
月 日至
日至 月
月 日这
日这 天的误差(模型预测数据与真实数据差值的绝对值与真实数据的比值)都小于
天的误差(模型预测数据与真实数据差值的绝对值与真实数据的比值)都小于 则认为模型可靠,请判断(2)的回归方程是否可靠?
则认为模型可靠,请判断(2)的回归方程是否可靠?(ii)
 年
年 月
月 日在人民政府的强力领导下,全国人民共同取了强力的预防“新冠肺炎”的措施,若采取措施
日在人民政府的强力领导下,全国人民共同取了强力的预防“新冠肺炎”的措施,若采取措施 天后,真实数据明显低于预测数据,则认为防护措施有效,请判断预防措施是否有效?并说明理由.
天后,真实数据明显低于预测数据,则认为防护措施有效,请判断预防措施是否有效?并说明理由.附:对于一组数据
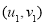 ,
,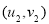 ,……,
,……, ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,平面
中,平面 底面ABCD,
底面ABCD,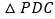 是等边三角形,底面ABCD为梯形,且
是等边三角形,底面ABCD为梯形,且 ,
, ,
, .
.
 Ⅰ
Ⅰ 证明:
证明: ;
; Ⅱ
Ⅱ 求A到平面PBD的距离.
求A到平面PBD的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)满足f(x+1)-f(x)=-2x+1,且f(2)=15.
(1)求函数f(x)的解析式;
(2) 令g(x)=(2-2m)x-f(x).
① 若函数g(x)在x∈[0,2]上是单调函数,求实数m的取值范围;
② 求函数g(x)在x∈[0,2]上的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
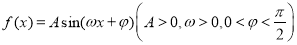 的部分图象如图所示,则下列叙述正确的是( )
的部分图象如图所示,则下列叙述正确的是( )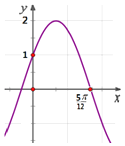
A.函数
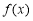 的图象可由
的图象可由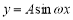 的图象向左平移
的图象向左平移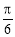 个单位得到
个单位得到B.函数
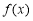 的图象关于直线
的图象关于直线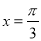 对称
对称C.函数
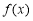 在区间
在区间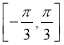 上是单调递增的
上是单调递增的D.函数
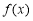 图象的对称中心为
图象的对称中心为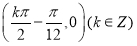
-
科目: 来源: 题型:
查看答案和解析>>【题目】中学生研学旅行是通过集体旅行、集中食宿方式开展的研究性学习和旅行体验相结合的校外教育活动,是学校教育和校外教育衔接的创新形式,是综合实践育人的有效途径.每年暑期都会有大量中学生参加研学旅行活动.为了解某地区中学生暑期研学旅行支出情况,在该地区各个中学随机抽取了部分中学生进行问卷调查,从中统计得到中学生暑期研学旅行支出(单位:百元)频率分布直方图如图所示.

(1)利用分层抽样在
 ,
, ,
, 三组中抽取5人,应从这三组中各抽取几人?
三组中抽取5人,应从这三组中各抽取几人?(2)从(1)抽取的5人中随机选出2人,对其消费情况进行进一步分析,求这2人不在同一组的概率;
(3)假设同组中的每个数据都用该区间的左端点值代替,估计该地区中学生暑期研学旅行支出的平均值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在棱长均为
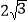 的四面体
的四面体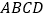 中,点
中,点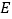 为
为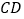 的中点,点
的中点,点 为
为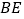 的中点.若点
的中点.若点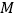 ,
,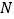 是平面
是平面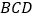 内的两动点,且
内的两动点,且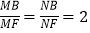 ,
,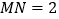 ,则
,则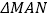 的面积为( )
的面积为( )A.
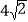 B. 3
B. 3C.
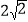 D. 2
D. 2
相关试题

