【题目】下列各组函数是同一函数的是( )
① ![]() 与
与 ![]() ;
;
②f(x)=|x|与 ![]() ;
;
③f(x)=x0与g(x)=1;
④f(x)=x2﹣2x﹣1与g(t)=t2﹣2t﹣1.
A.①②
B.①③
C.②④
D.③④
参考答案:
【答案】C
【解析】解:① ![]() 与
与 ![]() 的定义域是{x:x≤0};而①
的定义域是{x:x≤0};而① ![]() =﹣x
=﹣x ![]() ,故这两个函数不是同一函数;
,故这两个函数不是同一函数;
②f(x)=|x|与 ![]() 的定义域都是R,
的定义域都是R, ![]() =|x|,这两个函数的定义域相同,对应法则也相同,故这两个函数是同一函数;
=|x|,这两个函数的定义域相同,对应法则也相同,故这两个函数是同一函数;
③f(x)=x0的定义域是{x:x≠0},而g(x)=1的定义域是R,故这两个函数不是同一函数;
④f(x)=x2﹣2x﹣1与g(t)=t2﹣2t﹣1.是同一函数.
故C正确.
【考点精析】解答此题的关键在于理解判断两个函数是否为同一函数的相关知识,掌握只有定义域和对应法则二者完全相同的函数才是同一函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=
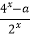 是奇函数,f(x)=lg(10x+1)+bx是偶函数.
是奇函数,f(x)=lg(10x+1)+bx是偶函数.
(1)求a+b的值.
(2)若对任意的t∈[0,+∞),不等式g(t2﹣2t)+g(2t2﹣k)>0恒成立,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知整数对按如图规律排成,照此规律,则第68个数对是 .
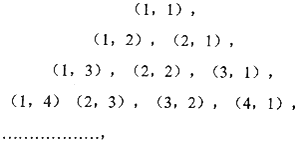
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知圆的参数方程为
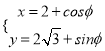 (
(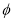 为参数),以直角坐标系的原点为极点,
为参数),以直角坐标系的原点为极点,  轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线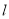 的极坐标方程为
的极坐标方程为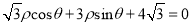 .
.(Ⅰ)将圆的参数方程化为普通方程,再化为极坐标方程;
(Ⅱ)若点
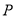 在直线
在直线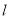 上,当点
上,当点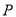 到圆的距离最小时,求点
到圆的距离最小时,求点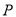 的极坐标.
的极坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知映射f:A→B,其中A=B=R,对应法则f:x→y=(
 )
) 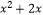 ,若对实数m∈B,在集合A中存在元素与之对应,则m的取值范围是( )
,若对实数m∈B,在集合A中存在元素与之对应,则m的取值范围是( )
A.(﹣∞,2]
B.[2,+∞)
C.(2,+∞)
D.(0,2] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x+
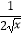 )n的展开式中的第二项和第三项的系数相等.
)n的展开式中的第二项和第三项的系数相等.
(1)求n的值;
(2)求展开式中所有二项式系数的和;
(3)求展开式中所有的有理项. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两名同学参加定点投篮测试,已知两人投中的概率分别是
 和
和 ,假设两人投篮结果相互没有影响,每人各次投球是否投中也没有影响.
,假设两人投篮结果相互没有影响,每人各次投球是否投中也没有影响.(Ⅰ)若每人投球3次(必须投完),投中2次或2次以上,记为达标,求甲达标的概率;
(Ⅱ)若每人有4次投球机会,如果连续两次投中,则记为达标.达标或能断定不达标,则终止投篮.记乙本次测试投球的次数为
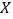 ,求
,求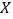 的分布列和数学期望
的分布列和数学期望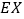 .
.
相关试题

