【题目】根据某水文观测点的历史统计数据,得到某河流水位X(单位:米)的频率分布直方图如图:将河流水位在以上6段的频率作为相应段的概率,并假设每年河流水位互不影响. 
(1)求未来三年,至多有1年河流水位X∈[27,31)的概率(结果用分数表示);
(2)该河流对沿河A企业影响如下:当X∈[23,27)时,不会造成影响;当X∈[27,31)时,损失10000元;当X∈[31,35)时,损失60000元,为减少损失,现有种应对方案: 方案一:防御35米的最高水位,需要工程费用3800元;
方案二:防御不超过31米的水位,需要工程费用2000元;
方案三:不采取措施;
试比较哪种方案较好,并请说理由.
参考答案:
【答案】
(1)解:由二项分布得,在未来3年,至多有1年河流水位X∈[27,31)的概率为:
P= ![]()
![]() +
+ ![]()
![]()
![]() =
= ![]() ,
,
所以在未来3年,至多有1年河流水位X∈[27,31)的概率为 ![]()
(2)解:由题意知,P(23≤X<27)=0.74,
P(27≤X<31)=0.25,
P(31≤X≤35)=0.01;
用X1、X2、X3分别表示采取方案一、二、三的损失,
由题意知,X1=3800,X2的分布列如下;
X2 | 2000 | 62000 |
P | 0.99 | 0.01 |
所以E(X2)=2000×0.99+62000×0.01=2600;
X3的分布列如下,
X3 | 0 | 10000 | 60000 |
P | 0.74 | 0.25 | 0.01 |
E(X3)=60000×0.01+10000×0.25=3100;
因为采用方案二的损失最小,所以采用方案二最好
【解析】(1)由二项分布求出未来3年,至多有1年河流水位X∈[27,31)的概率值;(2)由随机变量的分布列与均值,计算方案一、二、三的损失是多少,比较选用哪种方案最好.
【考点精析】本题主要考查了频率分布直方图的相关知识点,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息才能正确解答此题.
-
科目: 来源: 题型:
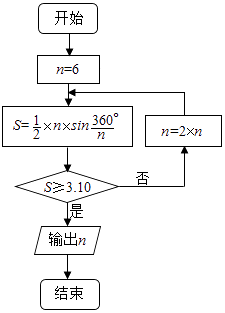
查看答案和解析>>【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为 . (参考数据:sin15°=0.2588,sin7.5°=0.1305)
-
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}满足an=
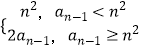 (n≥2),若{an}为等比数列,则a1的取值范围是 .
(n≥2),若{an}为等比数列,则a1的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=60°,D是BC上一点,AB=31,BD=20,AD=21.
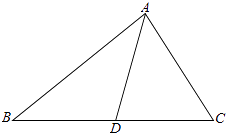
(1)求cos∠B的值;
(2)求sin∠BAC的值和边BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥PB,PC=2.

(1)求证:平面PAB⊥平面ABCD;
(2)若PA=PB,求二面角A﹣PC﹣D的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E:
 +
+  =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 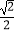 ,直线x+y+
,直线x+y+  =0与椭圆E仅有一个公共点.
=0与椭圆E仅有一个公共点.
(1)求椭圆E的方程;
(2)直线l被圆O:x2+y2=3所截得的弦长为3,且与椭圆E交于A、B两点,求△ABO面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形
 的三边长是公差为2的等差数列,且最大角的正弦值为
的三边长是公差为2的等差数列,且最大角的正弦值为 ,则这个三角形的周长是( )
,则这个三角形的周长是( )A. 18 B. 15 C. 21 D. 24
相关试题

