【题目】已知椭圆C: ![]() (a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(1)求椭圆的方程;
(2)若直线l与椭圆交于两点M,N(M,N不同于点A),若 ![]()
![]() =0,
=0, ![]() =
= ![]() ;
;
①求证:直线l过定点;并求出定点坐标;
②求直线AT的斜率的取值范围.
参考答案:
【答案】
(1)
解:由题意可知:a=2,
令x=c,代入椭圆方程,解得:y= ![]() ,则丨PQ丨=
,则丨PQ丨= ![]() =3,
=3,
则b= ![]() ,
,
∴椭圆的标准方程为: ![]()
(2)
解:①当直线MN斜率不存在时,设lMN:x=m,
则 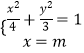 ,解得:y=
,解得:y= ![]() ,则丨MN丨=2
,则丨MN丨=2 ![]() ,
,
设直线MN与x轴交于点B,丨丨MB=丨AM丨即 ![]() =2﹣m,
=2﹣m,
∴m= ![]() 或m=2(舍),
或m=2(舍),
∴直线lMN过定点( ![]() ,0);
,0);
当直线MN斜率存在时,设直线MN斜率为k,
设M(x1,y1),N(x2,y2),则直线MN:y=kx+b,
与椭圆方程 ![]() ,联立,消取y整理得(4k2+3)x2+8kbx+4k2﹣12=0,
,联立,消取y整理得(4k2+3)x2+8kbx+4k2﹣12=0,
∴x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
△>0,k∈R,
![]()
![]() =0,(x1﹣2,y1)(x2﹣2,y2)=0,
=0,(x1﹣2,y1)(x2﹣2,y2)=0,
即x1x2﹣2(x1+x2)+4+y1y2=0,
y1y2=(kx1+b)(kx2+b)=k2x1x2+kb(x1+x2)+b2= ![]() ,
,
∴7b2+4k2+16kb=0,则b=﹣ ![]() k,或b=﹣2k,
k,或b=﹣2k,
∴lMN:y=k(x﹣ ![]() )或y=k(x﹣2),
)或y=k(x﹣2),
∴直线lMN过定点( ![]() ,0)或(2,0);
,0)或(2,0);
综合知,直线过定点( ![]() ,0);
,0);
②T为MN中点,T( ![]() ,
, ),则T(﹣
![]() ,
, ![]() ),
),
∴kAT= 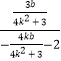 =
= ![]() ,
,
由b=﹣ ![]() ,则kAT=
,则kAT= ![]() ,
,
当k=0时,kAT=0,
当k≠0时,k∈R,kAT= ![]() =
= ![]() ,
,
由8k+ ![]() ≥2
≥2 ![]() =2
=2 ![]() ,
,
或8k+ ![]() ≤﹣2
≤﹣2 ![]() =﹣2
=﹣2 ![]() ,
,
∴kAT∈[﹣ ![]() ,
, ![]() ],
],
直线AT的斜率的取值范围为[﹣ ![]() ,
, ![]() ]
]
【解析】(1)由a=2,则椭圆的通径丨PQ丨= ![]() ,代入即可求得b的值,即可取得椭圆的方程;(2)当直线MN斜率不存在时,将x=m代入椭圆方程,则
,代入即可求得b的值,即可取得椭圆的方程;(2)当直线MN斜率不存在时,将x=m代入椭圆方程,则 ![]() =2﹣m,即可求得m的值,即可求得直线恒过定点;当斜率存在,设直线方程y=kx+b,代入椭圆方程,由韦达定理,向量的坐标运算,即可求得b=﹣
=2﹣m,即可求得m的值,即可求得直线恒过定点;当斜率存在,设直线方程y=kx+b,代入椭圆方程,由韦达定理,向量的坐标运算,即可求得b=﹣ ![]() k,或b=﹣2k,即可求得直线方程,则直线过定点(
k,或b=﹣2k,即可求得直线方程,则直线过定点( ![]() ,0);(3)利用中点坐标公式求得T坐标,利用直线的斜率公式,kAT=
,0);(3)利用中点坐标公式求得T坐标,利用直线的斜率公式,kAT= ![]() =
= ![]() ,分类当k=0,kAT=0,当k≠0时,利用基本不等式的性质,即可求得直线AT的斜率的取值范围.
,分类当k=0,kAT=0,当k≠0时,利用基本不等式的性质,即可求得直线AT的斜率的取值范围.
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥S﹣ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若
 =t
=t  .
. 
(1)当t= 时,求证:平面SAE⊥平面MNPQ;
时,求证:平面SAE⊥平面MNPQ;
(2)是否存在实数t,使得二面角M﹣PQ﹣A的平面角的余弦值为 ?若存在,求出实数t的值;若不存在,说明理由.
?若存在,求出实数t的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】北京时间3月10日,CBA半决赛开打,采用7局4胜制(若某对取胜四场,则终止本次比赛,并获得进入决赛资格),采用2﹣3﹣2的赛程,辽宁男篮将与新疆男篮争夺一个决赛名额,由于新疆队常规赛占优,决赛时拥有主场优势(新疆先两个主场,然后三个客场,再两个主场),以下是总决赛赛程:
日期
比赛队
主场
客场
比赛时间
比赛地点
17年3月10日
新疆﹣辽宁
新疆
辽宁
20:00
乌鲁木齐
17年3月12日
新疆﹣辽宁
新疆
辽宁
20:00
乌鲁木齐
17年3月15日
辽宁﹣新疆
辽宁
新疆
20:00
本溪
17年3月17日
辽宁﹣新疆
辽宁
新疆
20:00
本溪
17年3月19日
辽宁﹣新疆
辽宁
新疆
20:00
本溪
17年3月22日
新疆﹣辽宁
新疆
辽宁
20:00
乌鲁木齐
17年3月24日
新疆﹣辽宁
新疆
辽宁
20:00
乌鲁木齐
(1)若考虑主场优势,每个队主场获胜的概率均为 ,客场取胜的概率均为
,客场取胜的概率均为  ,求辽宁队以比分4:1获胜的概率;
,求辽宁队以比分4:1获胜的概率;
(2)根据以往资料统计,每场比赛组织者可获得门票收入50万元(与主客场无关),若不考虑主客场因素,每个队每场比赛获胜的概率均为 ,设本次半决赛中(只考虑这两支队)组织者所获得的门票收入为X,求X的分布列及数学期望.
,设本次半决赛中(只考虑这两支队)组织者所获得的门票收入为X,求X的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
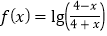 ,其中
,其中
(1)判断并证明函数
 的奇偶性;
的奇偶性;(2)判断并证明函数
 在
在 上的单调性;
上的单调性;(3)是否存在这样的负实数
 ,使
,使 对一切
对一切 恒成立,若存在,试求出
恒成立,若存在,试求出 取值的集合;若不存在,说明理由
取值的集合;若不存在,说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+(x﹣1)ex .
(1)当a=﹣ 时,求f(x)在点P(1,f(1))处的切线方程;
时,求f(x)在点P(1,f(1))处的切线方程;
(2)讨论f(x)的单调性;
(3)当﹣ <a<﹣
<a<﹣  时,f(x)是否存在极值?若存在,求所有极值的和的取值范围.
时,f(x)是否存在极值?若存在,求所有极值的和的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C1的参数方程为
 (θ为参数),曲线 C2的极坐标方程为ρcosθ﹣
(θ为参数),曲线 C2的极坐标方程为ρcosθ﹣  ρsinθ﹣4=0.
ρsinθ﹣4=0.
(1)求曲线C1的普通方程和曲线 C2的直角坐标方程;
(2)设P为曲线C1上一点,Q为曲线 C2上一点,求|PQ|的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 ,直线
,直线 ,
,  .
.(1)求证:对
 ,直线
,直线 与圆
与圆 总有两个不同的交点
总有两个不同的交点 ;
;(2)求弦
 的中点
的中点 的轨迹方程,并说明其轨迹是什么曲线.
的轨迹方程,并说明其轨迹是什么曲线.
相关试题

