【题目】已知圆![]() ,直线
,直线![]() ,
, ![]() .
.
(1)求证:对![]() ,直线
,直线![]() 与圆
与圆![]() 总有两个不同的交点
总有两个不同的交点![]() ;
;
(2)求弦![]() 的中点
的中点![]() 的轨迹方程,并说明其轨迹是什么曲线.
的轨迹方程,并说明其轨迹是什么曲线.
参考答案:
【答案】(1)见解析(2) ![]() 的轨迹方程是
的轨迹方程是![]() ,它是一个以
,它是一个以![]() 为圆心,以
为圆心,以![]() 为半径的圆
为半径的圆
【解析】试题分析:(1)利用圆心到直线的距离与圆的半径之间的关系,即可判定直线![]() 与圆
与圆![]() 总有两个不同的交点;
总有两个不同的交点;
(2)设中点为![]() ,当直线
,当直线![]() 的斜率存在时,利用∵
的斜率存在时,利用∵![]() ,化简得
,化简得![]() ;当直线
;当直线![]() 的斜率不存在时,
的斜率不存在时, ![]() ,此时中点为
,此时中点为![]() ,即可得到中点的轨迹方程;
,即可得到中点的轨迹方程;
试题解析:
证明:(1)圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,
,
所以圆心![]() 到直线
到直线![]() 的距离
的距离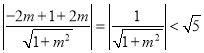 .
.
所以直线![]() 与圆
与圆![]() 相交,即直线
相交,即直线![]() 与圆
与圆![]() 总有两个不同的交点;
总有两个不同的交点;
(2)设中点为![]() ,
,
因为直线![]() 恒过定点
恒过定点![]() ,
,
当直线![]() 的斜率存在时,
的斜率存在时, ![]() ,又
,又![]() ,
,
∵![]() ,∴
,∴![]()
化简得![]() .
.
当直线![]() 的斜率不存在时,
的斜率不存在时, ![]() ,
,
此时中点为![]() ,也满足上述方程.
,也满足上述方程.
所以![]() 的轨迹方程是
的轨迹方程是![]() ,
,
它是一个以![]() 为圆心,以
为圆心,以![]() 为半径的圆.
为半径的圆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 (a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(1)求椭圆的方程;
(2)若直线l与椭圆交于两点M,N(M,N不同于点A),若
 =0,
=0,  =
=  ;
;
①求证:直线l过定点;并求出定点坐标;
②求直线AT的斜率的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+(x﹣1)ex .
(1)当a=﹣ 时,求f(x)在点P(1,f(1))处的切线方程;
时,求f(x)在点P(1,f(1))处的切线方程;
(2)讨论f(x)的单调性;
(3)当﹣ <a<﹣
<a<﹣  时,f(x)是否存在极值?若存在,求所有极值的和的取值范围.
时,f(x)是否存在极值?若存在,求所有极值的和的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C1的参数方程为
 (θ为参数),曲线 C2的极坐标方程为ρcosθ﹣
(θ为参数),曲线 C2的极坐标方程为ρcosθ﹣  ρsinθ﹣4=0.
ρsinθ﹣4=0.
(1)求曲线C1的普通方程和曲线 C2的直角坐标方程;
(2)设P为曲线C1上一点,Q为曲线 C2上一点,求|PQ|的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设z1 , z2是复数,则下列命题中的假命题是( )
A.若|z1﹣z2|=0,则 =
= 
B.若z1= ,则
,则  =z2
=z2
C.若|z1|=|z2|,则z1 =z2
=z2 
D.若|z1|=|z2|,则z12=z22 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体ABCD﹣A1B1C1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN=
 ,则MN与平面BB1C1C的位置关系为( )
,则MN与平面BB1C1C的位置关系为( )
A.相交
B.平行
C.垂直
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣1|﹣|2x+1|的最大值为m
(1)作函数f(x)的图象
(2)若a2+b2+2c2=m,求ab+2bc的最大值.
相关试题

