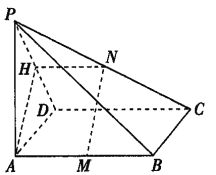
【题目】如图,已知点P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点.

(1)求证:MN∥平面PAD;
(2)在PB上确定一个点Q,使平面MNQ∥平面PAD.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)取PD的中点H,易证得AMNH为平行四边形,从而证得MN∥AH,即证得结论;
(2)由平面MNQ∥平面PAD,则应有MQ∥PA,利用中位线定理可确定位置.
(1)如图,取PD的中点H,
连接AH、NH.由N是PC的中点,H是PD的中点,知NH∥DC,NH=![]() DC.
DC.
由M是AB的中点,知AM∥DC,AM=![]() DC
DC
. 
∴NH∥AM,NH=AM,所以AMNH为平行四边形.
∴MN∥AH.
由MN平面PAD,AH平面PAD,
知MN∥平面PAD.
(2)若平面MNQ∥平面PAD,则应有MQ∥PA,
∵M是AB中点,∴Q是PB的中点.
即当Q为PB的中点时,平面MNQ∥平面PAD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在极坐标系中,已知曲线C1:ρ=2cosθ,将曲线C1上的点向左平移一个单位,然后纵坐标不变,横坐标伸长到原来的2倍,得到曲线C,又已知直线l:
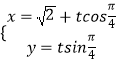 (t是参数),且直线l与曲线C交于A,B两点.
(t是参数),且直线l与曲线C交于A,B两点.
(1)求曲线C的直角坐标方程,并说明它是什么曲线;
(2)设定点P(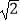 ,0),求|PA|+|PB|.
,0),求|PA|+|PB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
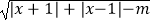 .
.
(1)当m=4时,求函数f(x)的定义域M;
(2)当a,b∈RM时,证明:2|a+b|<|4+ab|. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是菱形,
是菱形, 为
为 的中点,
的中点, 为
为 的中点.证明:直线
的中点.证明:直线 平面
平面 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
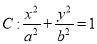 (a>b>0)的焦点在圆x2+y2=3上,且离心率为
(a>b>0)的焦点在圆x2+y2=3上,且离心率为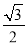 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)过原点O的直线l与椭圆C交于A,B两点,F为右焦点,若△FAB为直角三角形,求直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作
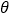 ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是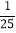 ,则
,则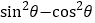 的值等于( )
的值等于( )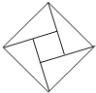
A. 1 B.
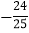 C.
C. 
 D.
D. 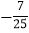
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
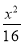 +
+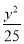 =1的焦点分别是
=1的焦点分别是 、
、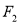 ,
, 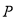 是椭圆上一点,若连结
是椭圆上一点,若连结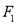 、
、 、
、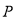 三点恰好能构成直角三角形,则点
三点恰好能构成直角三角形,则点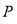 到
到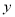 轴的距离是( )
轴的距离是( )A.
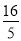 B.
B. 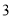 C.
C. 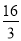 D.
D. 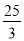
相关试题

