【题目】已知椭圆![]() +
+![]() =1的焦点分别是
=1的焦点分别是![]() 、
、![]() ,
, ![]() 是椭圆上一点,若连结
是椭圆上一点,若连结![]() 、
、![]() 、
、![]() 三点恰好能构成直角三角形,则点
三点恰好能构成直角三角形,则点![]() 到
到![]() 轴的距离是( )
轴的距离是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】椭圆![]() +
+![]() =1的焦点在
=1的焦点在![]() 轴上,且为
轴上,且为![]() ,且
,且![]() ,第一种情况,两焦点连线段
,第一种情况,两焦点连线段![]() 为直角边,则
为直角边,则![]() 点纵坐标为
点纵坐标为![]() ,则令
,则令![]() 代入椭圆方程,可得
代入椭圆方程,可得![]() 到
到![]() 轴距离为
轴距离为![]() ,第二种情况,两焦点连线段
,第二种情况,两焦点连线段![]() 为斜边,设
为斜边,设![]() ,则
,则
![]() ,即为
,即为![]() ,联立椭圆方程
,联立椭圆方程![]() +
+![]() =1,则无解,故点
=1,则无解,故点![]() 到到
到到![]() 轴距离为
轴距离为![]() ,故选A.
,故选A.
【方法点晴】本题主要考查利用椭圆的方程以及椭圆的简单性质,属于中档题.求解与椭圆性质有关的问题时要结合图形进行分析,既使不画出图形,思考时也要联想到图形,当涉及顶点、焦点、实轴、虚轴、离心率等双曲线的基本量时,要理清它们之间的关系,挖掘出它们之间的内在联系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点.

(1)求证:MN∥平面PAD;
(2)在PB上确定一个点Q,使平面MNQ∥平面PAD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
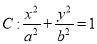 (a>b>0)的焦点在圆x2+y2=3上,且离心率为
(a>b>0)的焦点在圆x2+y2=3上,且离心率为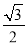 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)过原点O的直线l与椭圆C交于A,B两点,F为右焦点,若△FAB为直角三角形,求直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在北京召开的第24届国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小的锐角记作
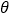 ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是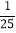 ,则
,则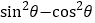 的值等于( )
的值等于( )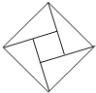
A. 1 B.
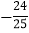 C.
C. 
 D.
D. 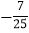
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC为锐角三角形,命题p:不等式logcosC
 >0恒成立,命题q:不等式logcosC
>0恒成立,命题q:不等式logcosC  >0恒成立,则复合命题p∨q、p∧q、¬p中,真命题的个数为( )
>0恒成立,则复合命题p∨q、p∧q、¬p中,真命题的个数为( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)判断并证明函数
 的奇偶性;
的奇偶性;(2)判断当
 时函数
时函数 的单调性,并用定义证明;
的单调性,并用定义证明;(3)若
 定义域为
定义域为 ,解不等式
,解不等式 .
.【答案】(1)奇函数(2)增函数(3)

【解析】试题分析:(1)判断与证明函数的奇偶性,首先要确定函数的定义域是否关于原点对称,再判断f(-x)与f(x)的关系,如果对定义域上的任意x,都满足f(-x)=f(x)就是偶函数,如果f(-x)=-f(x)就是奇函数,否则是非奇非偶函数。(2)利函数单调性定义证明单调性,按假设,作差,化简,判断,下结论五个步骤。(3)由(1)(2)奇函数
 在(-1,1)为单调函数,
在(-1,1)为单调函数,原不等式变形为f(2x-1)<-f(x),即f(2x-1)<f(-x),再由函数的单调性及定义(-1,1)求解得x范围。
试题解析:(1)函数
 为奇函数.证明如下:
为奇函数.证明如下: 定义域为
定义域为
又

 为奇函数
为奇函数 (2)函数
 在(-1,1)为单调函数.证明如下:
在(-1,1)为单调函数.证明如下:任取
 ,则
,则

 ,
, 

即

故
 在(-1,1)上为增函数
在(-1,1)上为增函数(3)由(1)、(2)可得
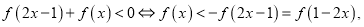 则
则 解得:
解得: 
所以,原不等式的解集为

【点睛】
(1)奇偶性:判断与证明函数的奇偶性,首先要确定函数的定义域是否关于原点对称,再判断f(-x)与f(x)的关系,如果对定义域上的任意x,都满足f(-x)=f(x)就是偶函数,如果f(-x)=-f(x)就是奇函数,否则是非奇非偶函数。
(2)单调性:利函数单调性定义证明单调性,按假设,作差,化简,定号,下结论五个步骤。
【题型】解答题
【结束】
22【题目】已知函数
 .
.(1)若
 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数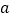 的值;
的值;(2)若
 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的 ,都有
,都有 ,求实数
,求实数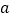 的取值范围;
的取值范围;(3)若
 ,且对任意的
,且对任意的 ,都存在
,都存在 ,使得
,使得 成立,求实数
成立,求实数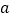 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设实数x,y满足不等式组
 ,(2,1)是目标函数z=﹣ax+y取最大值的唯一最优解,则实数a的取值范围是( )
,(2,1)是目标函数z=﹣ax+y取最大值的唯一最优解,则实数a的取值范围是( )
A.(0,1)
B.(0,1]
C.(﹣∞,﹣2)
D.(﹣∞,﹣2]
相关试题

