【题目】设函数f(x)= ![]() .
.
(1)当m=4时,求函数f(x)的定义域M;
(2)当a,b∈RM时,证明:2|a+b|<|4+ab|.
参考答案:
【答案】
(1)解:当m=4时,由|x+1|+|x﹣1|≥4,
等价于 ![]() 或
或 ![]() 或
或 ![]() ,
,
解得x≤﹣2或x≥2或x∈.
则不等式的解集为M={x|x≤﹣2或x≥2}
(2)解:证明:当a,b∈CRM时,即﹣2<a,b<2,
所以4(a+b)2﹣(4+ab)2=4(a2+2ab+b2)﹣(16+8ab+a2b2)
=4a2+4b2﹣16﹣a2b2=(a2﹣4)(4﹣b2)<0,所以4(a+b)2<(4+ab)2,
即2|a+b|<|4+ab|
【解析】(1)由题意和二次根式的被开方数非负,可得|x+1|+|x﹣1|≥4,运用绝对值的意义和对x讨论,解不等式即可得到所求定义域;(2)可得﹣2<a,b<2,要证2|a+b|<|4+ab|,可证4(a+b)2<(4+ab)2 , 作差4(a+b)2﹣(4+ab)2 , 运用平方差和因式分解,即可得证.
【考点精析】利用函数的定义域及其求法对题目进行判断即可得到答案,需要熟知求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
-
科目: 来源: 题型:
查看答案和解析>>【题目】a、b、c为三条不重合的直线,α、β、γ为三个不重合的平面,现给出六个命题.
①
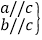 a∥b; ②
a∥b; ②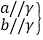 a∥b; ③
a∥b; ③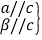 α∥β;
α∥β;④
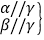 α∥β; ⑤
α∥β; ⑤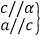 a∥α; ⑥
a∥α; ⑥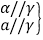 a∥α,
a∥α,其中正确的命题是________.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知圆O1与圆O2相交于A,B两点,过点A作圆O1的切线交圆O2于点C,过点B作两圆的割线,分别交圆O1 , 圆O2于点D,E,DE与AC相交于点P.
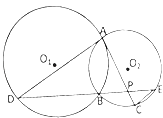
(1)求证:AD∥EC;
(2)若AD是圆O2的切线,且PA=3,PC=1,AD=6,求DB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在极坐标系中,已知曲线C1:ρ=2cosθ,将曲线C1上的点向左平移一个单位,然后纵坐标不变,横坐标伸长到原来的2倍,得到曲线C,又已知直线l:
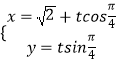 (t是参数),且直线l与曲线C交于A,B两点.
(t是参数),且直线l与曲线C交于A,B两点.
(1)求曲线C的直角坐标方程,并说明它是什么曲线;
(2)设定点P(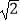 ,0),求|PA|+|PB|.
,0),求|PA|+|PB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是菱形,
是菱形, 为
为 的中点,
的中点, 为
为 的中点.证明:直线
的中点.证明:直线 平面
平面 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点.

(1)求证:MN∥平面PAD;
(2)在PB上确定一个点Q,使平面MNQ∥平面PAD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
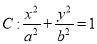 (a>b>0)的焦点在圆x2+y2=3上,且离心率为
(a>b>0)的焦点在圆x2+y2=3上,且离心率为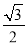 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)过原点O的直线l与椭圆C交于A,B两点,F为右焦点,若△FAB为直角三角形,求直线l的方程.
相关试题

