【题目】【2017届湖北省荆、荆、襄、宜四地七校考试联盟高三2月联考数学(文)】已知函数![]() .
.
(Ⅰ)讨论函数![]() 的极值点的个数;
的极值点的个数;
(Ⅱ)若![]() 有两个极值点
有两个极值点![]() ,证明:
,证明:![]() .
.
参考答案:
【答案】(Ⅰ)(ⅰ)![]()
![]()
![]() 时,
时,![]()
(ⅲ)当![]() 时,
时,![]()
【解析】试题分析:(Ⅰ)先求导数,再确定导函数零点情况,这需分类讨论:一次与二次的讨论,二次中有根与无根的讨论,两根情况分相等、一正一负、两不等正根,最后根据对应情况确定导函数符号变化规律,确定对应极值点个数;(Ⅱ)由(Ⅰ)先确定![]()
![]()
![]() 满足条件,再化简
满足条件,再化简![]() 为
为![]()
试题解析:解:(Ⅰ)由![]() 得,
得,
![]()
(ⅰ)![]()
![]() ,
,![]()
所以![]()
![]()
![]()
(ⅱ)![]()
![]()
![]() ,得
,得![]()
显然,![]() ,所以
,所以![]() ,
,
![]()
![]() 取得极小值,
取得极小值,![]()
(ⅲ)![]()
![]()
![]() 在
在![]()
![]()
当![]() 时,
时,![]()
![]() ,得
,得![]()
当![]() 和
和![]() 时
时![]() ,
,![]() 时,
时,![]() ,所以
,所以![]()
![]() 取得极小值,在
取得极小值,在![]() 取得极大值,所以
取得极大值,所以![]()
综上可知:(ⅰ)![]()
![]()
(ⅱ) 当![]() 时,
时,![]()
(ⅲ)当![]() 时,
时,![]()
(Ⅱ)由(Ⅰ)知,当且仅当![]() 时,
时,![]()
![]() 和极大值点
和极大值点![]() ,且
,且
![]() 是方程
是方程![]() 的两根,所以
的两根,所以![]() ,
,
![]()
![]()
![]() ,
,
设![]() ,
,![]() ,
,
所以![]() 时,
时,![]()
![]() ,则
,则![]()
所以![]() 得证.
得证.
-
科目: 来源: 题型:
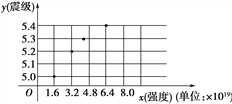
查看答案和解析>>【题目】某地区发生里氏8.0级特大地震.地震专家对发生的余震进行了监测,记录的部分数据如下表:
强度(J)
1.6×1019
3.2×1019
4.5×1019
6.4×1019
震级(里氏)
5.0
5.2
5.3
5.4
注:地震强度是指地震时释放的能量.
地震强度(x)和震级(y)的模拟函数关系可以选用y=alg x+b(其中a,b为常数).利用散点图(如图)可知a的值等于________.(取lg 2=0.3进行计算)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱锥
 的直观图和三视图如下:
的直观图和三视图如下: (1)求证:
 底面
底面 ;
;(2)求三棱锥
 的体积;
的体积;(3)求三棱锥
 的侧面积.
的侧面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量a=(x+z,3),b=(2,y-z),且a⊥b.若x,y满足不等式|x|+|y|≤1,则z的取值范围是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面α和β,在平面α内任取一条直线a,在β内总存在直线b∥a,则α与β的位置关系是____(填“平行”或“相交”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
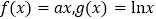 ,(
,(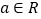 ).
).(1)若函数
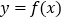 与
与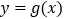 的图象在
的图象在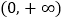 上有两个不同的交点,求实数
上有两个不同的交点,求实数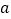 的取值范围;
的取值范围;(2)若在
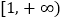 上不等式
上不等式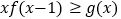 恒成立,求实数
恒成立,求实数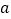 的取值范围;
的取值范围;(3)证明:对于
 时,任意
时,任意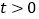 ,不等式
,不等式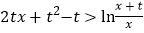 恒成立.
恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司试销某种“上海世博会”纪念品,每件按30元销售,可获利50%,设每件纪念品的成本为a元.
(1)试求a的值;
(2)公司在试销过程中进行了市场调查,发现销售量y(件)与每件售价x(元)满足关系y=-10x+800.设每天销售利润为W(元),求每天销售利润W(元)与每件售价x(元)之间的函数解析式;当每件售价为多少时,每天获得的利润最大?最大利润是多少?
相关试题

