【题目】某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段。现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.
分数(分数段) | 频数(人数) | 频率 |
[60,70) | ① | 0.16 |
[70,80) | 22 | ② |
[80,90) | 14 | 0.28 |
[90,100] | ③ | ④ |
合 计 | 50 | 1 |
(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(2)决赛规则如下:参加决赛的每位同学依次口答4道小题,答对2道题就终止答题,并获得一等奖。如果前三道题都答错,就不再答第四题。某同学进入决赛,每道题答对的概率![]() 的值恰好与频率分布表中不少于80分的频率的值相同.
的值恰好与频率分布表中不少于80分的频率的值相同.
①求该同学恰好答满4道题而获得一等奖的概率;
②记该同学决赛中答题个数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考答案:
【答案】(1)①8 ②0.44 ③6 ④0.12;(2)①0.1728;②见解析.
【解析】试题分析:(1)根据样本容量,频率和频数之间的关系得到要求的几个数据,注意第三个数据是用样本容量减去其他三个数得到;(2)①该同学恰好答满![]() 道题而获得一等奖,即前
道题而获得一等奖,即前![]() 道题中刚好答对
道题中刚好答对![]() 道,第
道,第![]() 道也能够答对才获得一等奖,根据相互独立事件的概率公式得到结果;②答对
道也能够答对才获得一等奖,根据相互独立事件的概率公式得到结果;②答对![]() 道题就终止答题,并获得一等奖,所以该同学答题个数为
道题就终止答题,并获得一等奖,所以该同学答题个数为![]() ,即
,即![]() ,结合变量对应的概率,写出分布列和期望.
,结合变量对应的概率,写出分布列和期望.
试题解析:(1)由图中数据知,样本容量为50,根据频率=![]() ,
,
①处=0.16×50=8;②处=![]() ;③处填:50﹣44=6;④处填:
;③处填:50﹣44=6;④处填:![]() .
.
故有:①8 ②0.44 ③6 ④0.12.
由(1),得![]()
①该同学恰好答满4道题而获得一等奖,即前3道题中刚好答对1道,
第4道也能够答对才获得一等奖,则有![]() ×0.4×0.62×0.4=0.1728.
×0.4×0.62×0.4=0.1728.
②由题设可知,该同学答题个数为2、3、4.即X=2、3、4,
![]()
![]()
![]()
| 2 | 3 | 4 |
| 0.16 | 0.408 | 0.432 |
分布列为:
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线
 上有一点
上有一点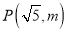 (
( ),点
),点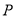 在
在 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线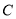 的右焦点,过点
的右焦点,过点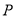 作双曲线
作双曲线 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为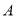 ,
, 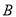 ,若平行四边形
,若平行四边形 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )A.
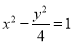 B.
B. 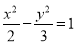 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
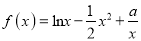 (
(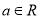 ,
, 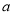 为常数),函数
为常数),函数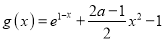 (
(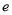 为自然对数的底).
为自然对数的底).(1)讨论函数
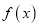 的极值点的个数;
的极值点的个数;(2)若不等式
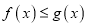 对
对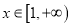 恒成立,求实数的
恒成立,求实数的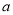 取值范围.
取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
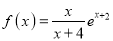 .
.(I)讨论函数的单调性,并证明当
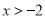 时,
时, 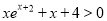 ;
;(Ⅱ)证明:当
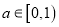 时,函数
时,函数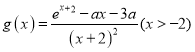 有最小值,设
有最小值,设 最小值为
最小值为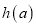 ,求函数
,求函数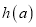 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】集合A={x|
 ≤0,x∈R},B={x||x﹣1|<2,x∈R}.
≤0,x∈R},B={x||x﹣1|<2,x∈R}.
(1)求A,B;
(2)求B∩(UA). -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果函数f(x)在[a,b]上存在x1 , x2(a<x1<x2<b)满足
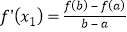
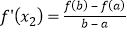 , ,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
, ,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
A.( ,
, )
)
B.( ,3)
,3)
C.( , 1)
, 1)
D.( , 1)
, 1) -
科目: 来源: 题型:
查看答案和解析>>【题目】某农户计划建造一个室内面积为800m2的矩形蔬菜温室,在温室外,沿左、右两侧与后侧各保留1m宽的通道,沿前侧保留3m的空地(如图所示),当矩形温室的长和宽分别为多少时,总占地面积最大?并求出最大值.

相关试题

