【题目】已知![]() 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线![]()
![]() 上有一点
上有一点![]() (
(![]() ),点
),点![]() 在
在![]() 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线![]() 的右焦点,过点
的右焦点,过点![]() 作双曲线
作双曲线![]() 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为![]() ,
, ![]() ,若平行四边形
,若平行四边形![]() 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. 
参考答案:
【答案】A
【解析】设平行线方程为![]() ,由
,由 ,解得
,解得![]() ,则
,则![]() ,又点
,又点![]() 到直线
到直线![]() 的距离
的距离 ,化简得:
,化简得: ![]() ,又
,又![]() ,又
,又![]() ,解得
,解得![]() ,所以方程是
,所以方程是![]() ,故选A.
,故选A.
【方法点晴】本题主要考查双曲线的简单性质、双曲线的渐近线及待定系数法求双曲线方程,属于中档题.求解与双曲线性质有关的问题时要结合图形进行分析,既使不画出图形,思考时也要联想到图形,当涉及顶点、焦点、实轴、虚轴、渐近线等双曲线的基本量时,要理清它们之间的关系,挖掘出它们之间的内在联系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱
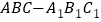 中,
中,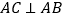 ,
,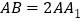 ,
,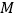 是
是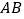 的中点,
的中点,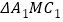 是等腰三角形,
是等腰三角形,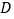 为
为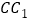 的中点,
的中点, 为
为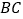 上一点.
上一点.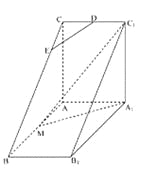
(I)若
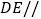 平面
平面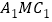 ,求
,求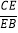 ;
;(II)平面
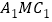 将三棱柱
将三棱柱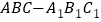 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,向量
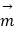 =(a+b,sinA﹣sinC),且
=(a+b,sinA﹣sinC),且 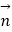 =(c,sinA﹣sinB),且
=(c,sinA﹣sinB),且 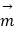 ∥
∥ 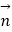 .
.
(1)求角B的大小;
(2)若a+c=8,求AC边上中线长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 :
: ,过焦点
,过焦点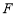 斜率大于零的直线
斜率大于零的直线 交抛物线于
交抛物线于 、
、 两点,且与其准线交于点
两点,且与其准线交于点 .
.
(Ⅰ)若线段
 的长为
的长为 ,求直线
,求直线 的方程;
的方程;(Ⅱ)在
 上是否存在点
上是否存在点 ,使得对任意直线
,使得对任意直线 ,直线
,直线 ,
, ,
, 的斜率始终成等差数列,若存在求点
的斜率始终成等差数列,若存在求点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】双流中学2016年高中毕业的大一学生假期参加社会实践活动,为提高某套丛书的销量,准备举办一场展销会,据市场调查,当每套丛书售价定为
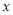 元时,销售量可达到
元时,销售量可达到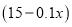 万套,现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10,假设不计其他成本,即销售每套丛书的利润=售价
万套,现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10,假设不计其他成本,即销售每套丛书的利润=售价 供货价格.问:
供货价格.问:(1)每套丛书售价定为100元时,书商所获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
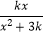 (k>0).
(k>0).
(1)若f(x)>m的解集为{x|x<﹣3或x>﹣2},求不等式5mx2+ x+3>0的解集;
x+3>0的解集;
(2)若存在x>3使得f(x)>1成立,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设fn(x)=(3n﹣1)x2﹣x(n∈N*),An={x|fn(x)<0}
(1)定义An={x|x1<x<x2}的长度为x2﹣x1 , 求An的长度;
(2)把An的长度记作数列{an},令bn=anan+1;
1°求数列{bn}的前n项和Sn;
2°是否存在正整数m,n(1<m<n),使得S1 , Sm , Sn成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
相关试题

