【题目】甲乙两支排球队进行比赛,先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是 ![]() ,其余每局比赛甲队获胜的概率都是
,其余每局比赛甲队获胜的概率都是 ![]() .设各局比赛结果相互独立.
.设各局比赛结果相互独立.
(1)分别求甲队3:0,3:1,3:2胜利的概率;
(2)若比赛结果3:0或3:1,则胜利方得3分,对方得0分;若比赛结果为3:2,则胜利方得2分,对方得1分,求乙队得分X的分布列及数学期望.
参考答案:
【答案】
(1)解:甲队获胜有三种情形,其每种情形的最后一局肯定是甲队胜
①3:0,概率为P1=( ![]() )3=
)3= ![]() ;
;
②3:1,概率为P2=C ![]() (
( ![]() )2×(1﹣
)2×(1﹣ ![]() )×
)× ![]() =
= ![]() ;
;
③3:2,概率为P3=C ![]() (
( ![]() )2×(1﹣
)2×(1﹣ ![]() )2×
)2× ![]() =
= ![]()
∴甲队3:0,3:1,3:2胜利的概率: ![]()
(2)解:乙队得分X,则X的取值可能为0,1,2,3.
由(1)知P(X=0)=P1+P2= ![]() ;
;
P(X=1)=P3= ![]() ;
;
P(X=2)=C ![]() (1﹣
(1﹣ ![]() )2×(
)2×( ![]() )2×
)2× ![]() =
= ![]() ;
;
P(X=3)=(1﹣ ![]() )3+C
)3+C ![]() (1﹣
(1﹣ ![]() )2×(
)2×( ![]() )×
)× ![]() =
= ![]() ;
;
则X的分布列为
X | 3 | 2 | 1 | 0 |
P |
|
|
|
|
E(X)=3× ![]() +2×
+2× ![]() +1×
+1× ![]() +0×
+0× ![]() =
= ![]()
【解析】(1)甲队获胜有三种情形,①3:0,②3:1,③3:2,其每种情形的最后一局肯定是甲队胜,分别求出相应的概率,最后根据互斥事件的概率公式求出甲队获得这次比赛胜利的概率;(2)X的取值可能为0,1,2,3,然后利用相互独立事件的概率乘法公式求出相应的概率,列出分布列,最后根据数学期望公式解之即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 过点
过点 ,其参数方程为
,其参数方程为 (
( 为参数,
为参数, ),以坐标原点为极点,以
),以坐标原点为极点,以 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出曲线
 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;(2)已知曲线
 和曲线
和曲线 交于
交于 ,
, 两点(
两点( 在
在 、
、 之间),且
之间),且 ,求实数
,求实数 的值.
的值. -
科目: 来源: 题型:
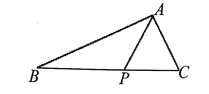
查看答案和解析>>【题目】如图,在
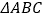 中,点
中,点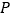 在
在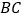 边上,
边上, ,
,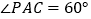 ,
,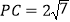 ,
,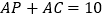 .
.
(1)求
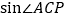 的值;
的值;(2)若
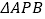 的面积是
的面积是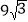 ,求
,求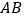 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在三棱锥P﹣ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
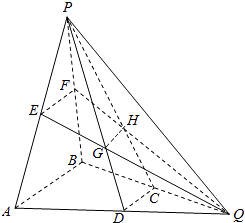
(1)求证:AB∥GH;
(2)求二面角D﹣GH﹣E的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组样本点
 ,其中
,其中 .根据最小二乘法求得的回归方程是
.根据最小二乘法求得的回归方程是 ,则下列说法正确的是( )
,则下列说法正确的是( )A. 若所有样本点都在
 上,则变量间的相关系数为1
上,则变量间的相关系数为1B. 至少有一个样本点落在回归直线
 上
上C. 对所有的预报变量
 ,
, 的值一定与
的值一定与 有误差
有误差D. 若
 斜率
斜率 ,则变量
,则变量 与
与 正相关
正相关 -
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列{an}的前n项和为Sn , 且S4=4S2 , a2n=2an+1.
(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Tn且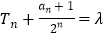 (λ为常数).令cn=b2n(n∈N*)求数列{cn}的前n项和Rn .
(λ为常数).令cn=b2n(n∈N*)求数列{cn}的前n项和Rn . -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。

(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
相关试题

