【题目】如图所示,在三棱锥P﹣ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH. 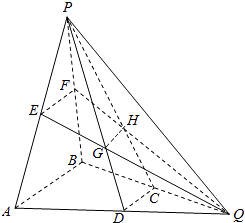
(1)求证:AB∥GH;
(2)求二面角D﹣GH﹣E的余弦值.
参考答案:
【答案】
(1)证明:如图,
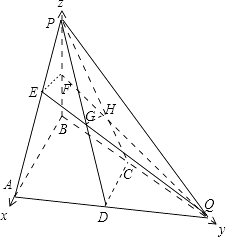
∵C,D为AQ,BQ的中点,∴CD∥AB,
又E,F分别AP,BP的中点,∴EF∥AB,
则EF∥CD.又EF平面EFQ,∴CD∥平面EFQ.
又CD平面PCD,且平面PCD∩平面EFQ=GH,∴CD∥GH.
又AB∥CD,∴AB∥GH
(2)解:由AQ=2BD,D为AQ的中点可得,三角形ABQ为直角三角形,
以B为坐标原点,分别以BA、BQ、BP所在直线为x、y、z轴建立空间直角坐标系,
设AB=BP=BQ=2,
则D(1,1,0),C(0,1,0),E(1,0,1),F(0,0,1),
因为H为三角形PBQ的重心,所以H(0, ![]() ,
, ![]() ).
).
则 ![]() ,
, ![]()
![]() ,
, ![]() .
.
设平面GCD的一个法向量为 ![]()
由 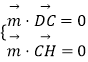 ,得
,得 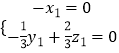 ,取z1=1,得y1=2.
,取z1=1,得y1=2.
所以 ![]() .
.
设平面EFG的一个法向量为 ![]()
由 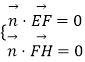 ,得
,得 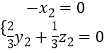 ,取z2=2,得y2=1.
,取z2=2,得y2=1.
所以 ![]() .
.
所以 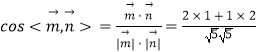 =
= ![]() .
.
则二面角D﹣GH﹣E的余弦值等于- ![]()
【解析】(1)由给出的D,C,E,F分别是AQ,BQ,AP,BP的中点,利用三角形中位线知识及平行公理得到DC平行于EF,再利用线面平行的判定和性质得到DC平行于GH,从而得到AB∥GH;(2)由题意可知BA、BQ、BP两两相互垂直,以B为坐标原点建立空间直角坐标系,设出BA、BQ、BP的长度,标出点的坐标,求出一些向量的坐标,利用二面角的两个面的法向量所成的角的余弦值求解二面角D﹣GH﹣E的余弦值.
【考点精析】解答此题的关键在于理解直线与平面平行的性质的相关知识,掌握一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】ΔABC的内角A,B,C的对边分别为a,b,c,根据下列条件解三角形,其中有两解的是
A. a=2,b=3,A=30°B. b=6,c=4,A=120°
C. a=4
 ,b=6,A=60°D. a=3,b=6,A=30°
,b=6,A=60°D. a=3,b=6,A=30° -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 过点
过点 ,其参数方程为
,其参数方程为 (
( 为参数,
为参数, ),以坐标原点为极点,以
),以坐标原点为极点,以 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出曲线
 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;(2)已知曲线
 和曲线
和曲线 交于
交于 ,
, 两点(
两点( 在
在 、
、 之间),且
之间),且 ,求实数
,求实数 的值.
的值. -
科目: 来源: 题型:
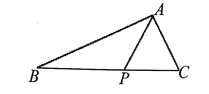
查看答案和解析>>【题目】如图,在
 中,点
中,点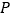 在
在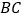 边上,
边上, ,
,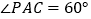 ,
,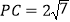 ,
,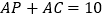 .
.
(1)求
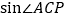 的值;
的值;(2)若
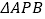 的面积是
的面积是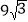 ,求
,求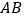 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两支排球队进行比赛,先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是
 ,其余每局比赛甲队获胜的概率都是
,其余每局比赛甲队获胜的概率都是  .设各局比赛结果相互独立.
.设各局比赛结果相互独立.
(1)分别求甲队3:0,3:1,3:2胜利的概率;
(2)若比赛结果3:0或3:1,则胜利方得3分,对方得0分;若比赛结果为3:2,则胜利方得2分,对方得1分,求乙队得分X的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组样本点
 ,其中
,其中 .根据最小二乘法求得的回归方程是
.根据最小二乘法求得的回归方程是 ,则下列说法正确的是( )
,则下列说法正确的是( )A. 若所有样本点都在
 上,则变量间的相关系数为1
上,则变量间的相关系数为1B. 至少有一个样本点落在回归直线
 上
上C. 对所有的预报变量
 ,
, 的值一定与
的值一定与 有误差
有误差D. 若
 斜率
斜率 ,则变量
,则变量 与
与 正相关
正相关 -
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列{an}的前n项和为Sn , 且S4=4S2 , a2n=2an+1.
(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Tn且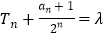 (λ为常数).令cn=b2n(n∈N*)求数列{cn}的前n项和Rn .
(λ为常数).令cn=b2n(n∈N*)求数列{cn}的前n项和Rn .
相关试题

