【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,且过点(1,
,且过点(1,![]() ).
).
(I)求椭圆C的方程;
(Ⅱ)设与圆O:x2+y2=![]() 相切的直线l交椭圆C与A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程.
相切的直线l交椭圆C与A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程.
参考答案:
【答案】(I)![]() (Ⅱ)△OAB面积的最大值为
(Ⅱ)△OAB面积的最大值为![]() ,此时直线方程
,此时直线方程![]()
【解析】
试题分析:(1)运用椭圆的离心率公式和点满足椭圆方程,解方程可得a,b,进而得到椭圆方程;(2)讨论①当k不存在时,②当k存在时,设直线为y=kx+m,A![]() ,B
,B![]() ,将直线y=kx+m代入椭圆方程,运用韦达定理和弦长公式,以及直线和圆相切的条件:d=r,结合基本不等式即可得到所求面积的最大值和直线l的方程
,将直线y=kx+m代入椭圆方程,运用韦达定理和弦长公式,以及直线和圆相切的条件:d=r,结合基本不等式即可得到所求面积的最大值和直线l的方程
试题解析:(1)由题意可得,e=![]() =
=![]() ,a2﹣b2=c2,点(1,
,a2﹣b2=c2,点(1,![]() )代入椭圆方程,可得
)代入椭圆方程,可得
![]() +
+![]() =1,解得a=
=1,解得a=![]() ,b=1,即有椭圆的方程为
,b=1,即有椭圆的方程为![]() ;
;
(2)①当k不存在时,x=±![]() 时,可得y=±
时,可得y=±![]() ,S△OAB=
,S△OAB=![]() ×
×![]() ×
×![]() =
=![]() ;
;
②当k存在时,设直线为y=kx+m,A(x1,y1),B(x2,y2),
将直线y=kx+m代入椭圆方程可得(1+3k2)x2+6kmx+3m2﹣3=0,
x1+x2=﹣![]() ,x1x2=
,x1x2=![]() ,
,
由直线l与圆O:x2+y2=![]() 相切,可得
相切,可得![]() =
=![]() ,即有4m2=3(1+k2),
,即有4m2=3(1+k2),
|AB|=![]()
![]() =
=![]()

=![]()
![]() =
=![]()
![]()
=![]()
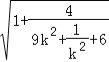 ≤
≤![]()
![]() =2,
=2,
当且仅当9k2=![]() 即k=±
即k=±![]() 时等号成立,可得S△OAB=
时等号成立,可得S△OAB=![]() |AB|r≤
|AB|r≤![]() ×2×
×2×![]() =
=![]() ,
,
即有△OAB面积的最大值为![]() ,此时直线方程y=±
,此时直线方程y=±![]() x±1.
x±1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.(本小题满分12分)
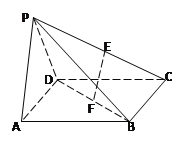
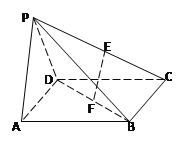
如图,四棱锥P—ABCD中,底面ABCD是边长为
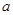 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=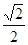 AD.
AD.(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 =(
=( 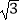 sinx,m+cosx),
sinx,m+cosx), 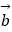 =(cosx,﹣m+cosx),且f(x)=
=(cosx,﹣m+cosx),且f(x)= 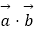
(1)求函数f(x)的解析式;
(2)当x∈[﹣ ,
,  ]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值.
]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
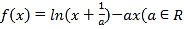 且
且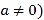
(1)讨论
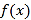 的单调区间;
的单调区间;(2)若直线
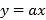 的图象恒在函数
的图象恒在函数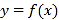 图象的上方,求
图象的上方,求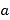 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的两个焦点是F1(﹣2,0),F2(2,0),且椭圆C经过点A(0,
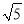 ).
).(1)求椭圆C的标准方程;
(2)若过椭圆C的左焦点F1(﹣2,0)且斜率为1的直线l与椭圆C交于P、Q两点,求线段PQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.(本小题满分12分)
如图,四棱锥P—ABCD中,底面ABCD是边长为
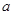 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=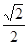 AD.
AD.(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
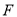 是拋物线
是拋物线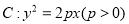 的焦点, 若点
的焦点, 若点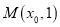 在
在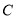 上,且
上,且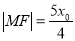 .
.(1)求
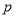 的值;
的值;(2)若直线
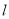 经过点
经过点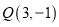 且与
且与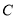 交于
交于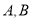 (异于
(异于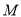 )两点, 证明: 直线
)两点, 证明: 直线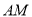 与直线
与直线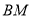 的斜率之积为常数.
的斜率之积为常数.
相关试题

