【题目】.(本小题满分12分)
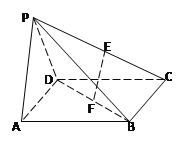
如图,四棱锥P—ABCD中,底面ABCD是边长为![]() 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=![]() AD.
AD.
(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.
参考答案:
【答案】解:(Ⅰ)证明:连接AC,则F是AC的中点,
E为PC的中点,故在![]() CPA中,EF//PA,
CPA中,EF//PA,
且PA![]() 平面PAD,EF
平面PAD,EF![]() 平面PAD,∴EF//平面PAD
平面PAD,∴EF//平面PAD
(Ⅱ)取AD的中点M,连接PM,∵PA=PD,∴PM⊥AD,又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,∴PM⊥平面ABCD.
在直角![]() PAM中,求得PM=
PAM中,求得PM=![]() ,∴
,∴![]()
![]() PM=
PM=![]()
【解析】试题分析:解:(Ⅰ)证明:连接AC,则F是AC的中点,
E为PC的中点,故在![]() CPA中,EF//PA,
CPA中,EF//PA,
且PA![]() 平面PAD,EF
平面PAD,EF![]() 平面PAD,∴EF//平面PAD
平面PAD,∴EF//平面PAD
(Ⅱ)取AD的中点M,连接PM,∵PA=PD,∴PM⊥AD,又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,∴PM⊥平面ABCD.
在直角![]() PAM中,求得PM=
PAM中,求得PM= ![]() ,∴
,∴![]()
![]() PM=
PM=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
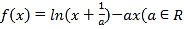 且
且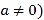
(1)讨论
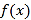 的单调区间;
的单调区间;(2)若直线
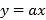 的图象恒在函数
的图象恒在函数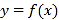 图象的上方,求
图象的上方,求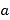 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
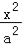 +
+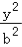 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为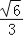 ,且过点(1,
,且过点(1,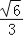 ).
).(I)求椭圆C的方程;
(Ⅱ)设与圆O:x2+y2=
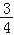 相切的直线l交椭圆C与A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程.
相切的直线l交椭圆C与A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的两个焦点是F1(﹣2,0),F2(2,0),且椭圆C经过点A(0,
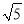 ).
).(1)求椭圆C的标准方程;
(2)若过椭圆C的左焦点F1(﹣2,0)且斜率为1的直线l与椭圆C交于P、Q两点,求线段PQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
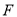 是拋物线
是拋物线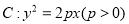 的焦点, 若点
的焦点, 若点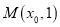 在
在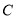 上,且
上,且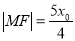 .
.(1)求
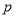 的值;
的值;(2)若直线
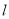 经过点
经过点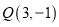 且与
且与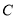 交于
交于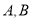 (异于
(异于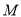 )两点, 证明: 直线
)两点, 证明: 直线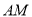 与直线
与直线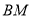 的斜率之积为常数.
的斜率之积为常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程2x2﹣(
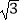 +1)x+m=0的两根为sinθ和cosθ,θ∈(0,π).求:
+1)x+m=0的两根为sinθ和cosθ,θ∈(0,π).求:
(1)m的值;
(2)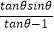 +
+ 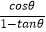 的值;
的值;
(3)方程的两根及此时θ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成
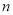 小块地,在总共
小块地,在总共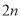 小块地中,随机选
小块地中,随机选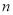 小块地种植品种甲,另外
小块地种植品种甲,另外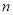 小块地种植品种乙.
小块地种植品种乙.(1)假设
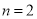 ,求第一大块地都种植品种甲的概率;
,求第一大块地都种植品种甲的概率;(2)试验时每大块地分成
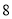 小块,即
小块,即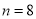 ,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:甲
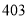
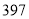
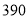
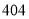
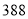
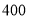
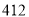
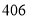
乙
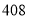
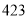
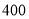
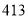
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
相关试题

