【题目】已知 ![]() =(
=( ![]() sinx,m+cosx),
sinx,m+cosx), ![]() =(cosx,﹣m+cosx),且f(x)=
=(cosx,﹣m+cosx),且f(x)= ![]()
(1)求函数f(x)的解析式;
(2)当x∈[﹣ ![]() ,
, ![]() ]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值.
]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值.
参考答案:
【答案】
(1)解:f(x)= ![]() ×
× ![]() =(
=( ![]() sinx,m+cosx)×(cosx,﹣m+cosx),
sinx,m+cosx)×(cosx,﹣m+cosx),
即 ![]() =
= ![]()
(2)解: ![]() =
= ![]() ,由
,由 ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
∴m=±2,∴fmax(x)=1+ ![]() ﹣4=﹣
﹣4=﹣ ![]() ,此时
,此时 ![]() ,
, ![]()
【解析】(1)f(x)= ![]() ×
× ![]() =(
=( ![]() sinx,m+cosx)×(cosx,﹣m+cosx)=
sinx,m+cosx)×(cosx,﹣m+cosx)= ![]() .`(2)函数f(x)=
.`(2)函数f(x)= ![]() ,根据
,根据 ![]() ,求得
,求得 ![]() ,得到
,得到 ![]() ,从而得到函数f(x)的最大值 及相应的x的值.
,从而得到函数f(x)的最大值 及相应的x的值.
【考点精析】本题主要考查了三角函数的最值的相关知识点,需要掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
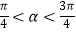 ,0<β<
,0<β<  ,cos(
,cos(  +α)=﹣
+α)=﹣ 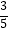 ,sin(
,sin( 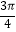 +β)=
+β)= 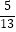 ,求sin(α+β)的值.
,求sin(α+β)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
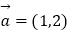 ,
, 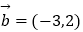 ,当k为何值时,
,当k为何值时,
(1)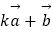 与
与 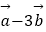 垂直?
垂直?
(2)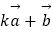 与
与 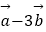 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
-
科目: 来源: 题型:
查看答案和解析>>【题目】.(本小题满分12分)
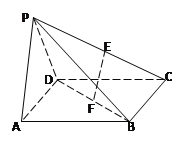
如图,四棱锥P—ABCD中,底面ABCD是边长为
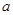 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=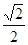 AD.
AD.(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
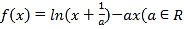 且
且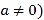
(1)讨论
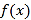 的单调区间;
的单调区间;(2)若直线
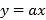 的图象恒在函数
的图象恒在函数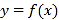 图象的上方,求
图象的上方,求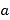 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
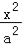 +
+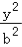 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为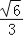 ,且过点(1,
,且过点(1,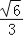 ).
).(I)求椭圆C的方程;
(Ⅱ)设与圆O:x2+y2=
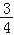 相切的直线l交椭圆C与A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程.
相切的直线l交椭圆C与A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的两个焦点是F1(﹣2,0),F2(2,0),且椭圆C经过点A(0,
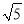 ).
).(1)求椭圆C的标准方程;
(2)若过椭圆C的左焦点F1(﹣2,0)且斜率为1的直线l与椭圆C交于P、Q两点,求线段PQ的长.
相关试题

