【题目】已知函数![]() ,且
,且![]() .
.
(1)若函数![]() 在区间
在区间![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)设函数![]() ,当
,当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1) 函数![]() 在区间
在区间![]() 上是减函数等价于
上是减函数等价于![]() 在区间
在区间![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,由二次函数知识可求
上恒成立,由二次函数知识可求![]() 的范围;
的范围;
(2)令![]() ,当
,当![]() 时,
时,![]() 恒成立等价于
恒成立等价于![]() 在区间
在区间![]() 上恒成立,求函数
上恒成立,求函数![]() 的导数,分类讨论研究函数在区间
的导数,分类讨论研究函数在区间![]() 的单调性求之即可.
的单调性求之即可.
试题解析:(1)∵函数![]() 在区间
在区间![]() 上是减函数,则
上是减函数,则![]() ,
,
即![]() 在
在![]() 上恒成立,当
上恒成立,当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() ,①若
,①若![]() ,则
,则![]() ,解得
,解得![]() ;
;
②若![]() ,则
,则![]() ,解得
,解得![]() .
.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)令![]() ,则
,则![]() ,根据题意,当
,根据题意,当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() .
.
①当![]() 时,
时,![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,所以不符题意.
,所以不符题意.
②当![]() 时,
时,![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() 所以不符题意.
所以不符题意.
③当![]() 时,
时,![]() 时,恒有
时,恒有![]() ,故
,故![]() 在
在![]() 上是减函数,于是“
上是减函数,于是“![]() 对任意
对任意![]() 都成立”的充要条件是
都成立”的充要条件是![]() ,即
,即![]() ,解得
,解得![]() ,故
,故![]() ,综上,
,综上,![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了传承经典,促进学生课外阅读,某校从高中年级和初中年级各随机抽取100名学生进行有关对中国四大名著常识了解的竞赛.图1和图2分别是高中年级和初中年级参加竞赛的学生成绩按照
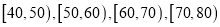 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.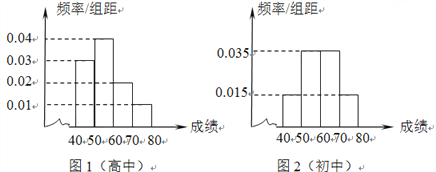
(1)分别计算参加这次知识竞赛的两个学段的学生的平均成绩;
(2)规定竞赛成绩达到
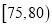 为优秀,经统计初中年级有3名男同学,2名女同学达到优秀,现从上述5人中任选两人参加复试,求选中的2人恰好都为女生的概率;
为优秀,经统计初中年级有3名男同学,2名女同学达到优秀,现从上述5人中任选两人参加复试,求选中的2人恰好都为女生的概率;(3)完成下列
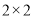 的列联表,并回答是否有99%的把握认为“两个学段的学生对四大名著的了解有差异”?
的列联表,并回答是否有99%的把握认为“两个学段的学生对四大名著的了解有差异”?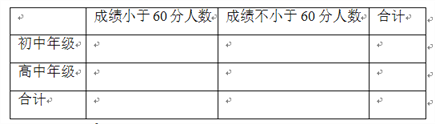
附:
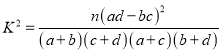
临界值表:
0.10
0.05
0.01
2.706
3.841
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数
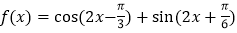 ,有下列结论:
,有下列结论:①
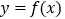 的最大值为
的最大值为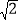 ;
;②
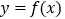 的最小正周期是
的最小正周期是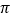 ;
;③
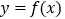 在区间
在区间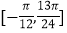 上是减函数;
上是减函数;④直线
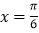 是函数
是函数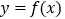 的一条对称轴方程.
的一条对称轴方程.其中正确结论的序号是__________.
-
科目: 来源: 题型:
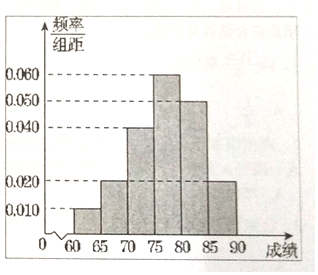
查看答案和解析>>【题目】在某次综合素质测试中,共设有60个考场,每个考场30名考生,在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考场中座位号为06的考生,统计了他们的成绩,得到如图所示的频率分布直方图.
问:
在这个调查采样中,采用的是什么抽样方法?
估计这次测试中优秀(80分及以上)的人数;
写出这60名考生成绩的众数、中位数、平均数的估计值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
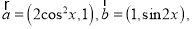 函数
函数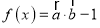
(1)
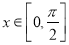 求函数
求函数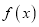 的值域;
的值域;(2)求方程
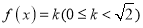 ,在
,在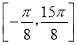 内的所有实数根之和.
内的所有实数根之和. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线
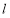 的参数方程为
的参数方程为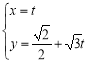 (
( 为参数),若以直角坐标系
为参数),若以直角坐标系 的
的 点为极点,
点为极点,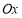 方向为极轴,选择相同的长度单位建立极坐标系,得曲线
方向为极轴,选择相同的长度单位建立极坐标系,得曲线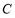 的极坐标方程为
的极坐标方程为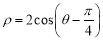 .
.(1)求直线
 的倾斜角和曲线
的倾斜角和曲线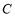 的直角坐标方程;
的直角坐标方程;(2)若直线
 与曲线
与曲线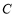 交于
交于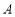 、
、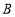 两点,设点
两点,设点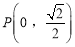 ,求
,求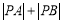 .
. -
科目: 来源: 题型:
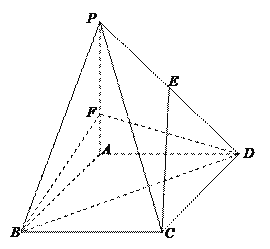
查看答案和解析>>【题目】如图,在边长为3的菱形ABCD中,∠ABC=60°,
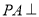 平面ABCD,且
平面ABCD,且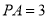 ,E为PD中点,F在棱PA上,且
,E为PD中点,F在棱PA上,且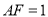 .
.(1)求证:CE∥平面BDF;
(2)求点P到平面BDF的距离.
相关试题

