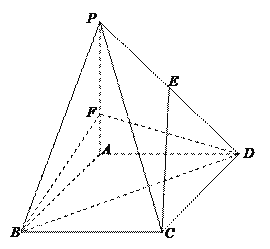
【题目】如图,在边长为3的菱形ABCD中,∠ABC=60°,![]() 平面ABCD,且
平面ABCD,且![]() ,E为PD中点,F在棱PA上,且
,E为PD中点,F在棱PA上,且![]() .
.
(1)求证:CE∥平面BDF;
(2)求点P到平面BDF的距离.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:
(1)利用题意取PF中点G,连接AC交BD于O点,连接FO,GC,EG
由题意易知平面EGC∥平面BDF, ![]() ,∴CE∥平面BDF
,∴CE∥平面BDF
(2)由题意利用体积相等,在四面体FABD中,易求得![]() ,
, ![]() ,∴P到平面BDF的距离等于
,∴P到平面BDF的距离等于![]()
试题解析:
(1)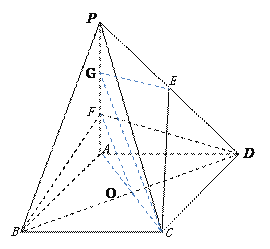
取PF中点G,连接AC交BD于O点,连接FO,GC,EG
由题意易知G为PF中点,又E为PD中点,所以GE∥FD,故
FO为三角形AGC的中位线,所以FO∥GC

所以面EGC∥平面BDF, ![]() ,∴CE∥平面BDF
,∴CE∥平面BDF
(2)由题意知点P到平面BDF的距离等于A到平面BDF的距离的两倍,记A到平面BDF的距离为h,则在四面体FABD中,易求得![]()
由体积自等得![]() ,
,
∴![]() ,∴P到平面BDF的距离等于
,∴P到平面BDF的距离等于![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
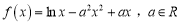 ,且
,且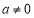 .
.(1)若函数
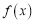 在区间
在区间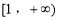 上是减函数,求实数
上是减函数,求实数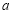 的取值范围;
的取值范围;(2)设函数
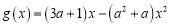 ,当
,当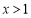 时,
时,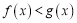 恒成立,求
恒成立,求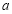 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
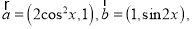 函数
函数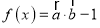
(1)
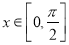 求函数
求函数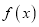 的值域;
的值域;(2)求方程
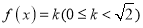 ,在
,在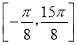 内的所有实数根之和.
内的所有实数根之和. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线
 的参数方程为
的参数方程为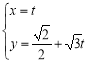 (
( 为参数),若以直角坐标系
为参数),若以直角坐标系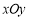 的
的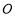 点为极点,
点为极点,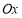 方向为极轴,选择相同的长度单位建立极坐标系,得曲线
方向为极轴,选择相同的长度单位建立极坐标系,得曲线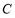 的极坐标方程为
的极坐标方程为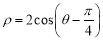 .
.(1)求直线
 的倾斜角和曲线
的倾斜角和曲线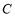 的直角坐标方程;
的直角坐标方程;(2)若直线
 与曲线
与曲线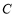 交于
交于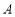 、
、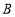 两点,设点
两点,设点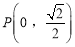 ,求
,求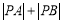 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
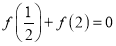 ,求
,求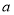 的值;
的值;(2)若存在
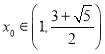 ,使函数
,使函数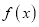 的图像在点
的图像在点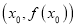 和点
和点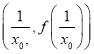 处的切线互相垂直,求
处的切线互相垂直,求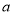 的取值范围;
的取值范围;(3)若函数
 在区间
在区间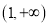 上有两个极值点,则是否存在实数
上有两个极值点,则是否存在实数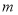 ,使
,使 对任意的
对任意的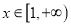 恒成立?若存在,求出
恒成立?若存在,求出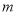 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一个八面体各棱长均为1,四边形ABCD为正方形,则下列命题中不正确的是
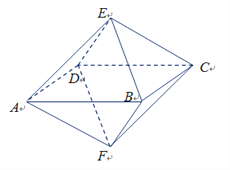
A. 不平行的两条棱所在直线所成的角为
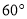 或
或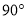 B. 四边形AECF为正方形
B. 四边形AECF为正方形C. 点A到平面BCE的距离为
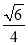 D. 该八面体的顶点在同一个球面上
D. 该八面体的顶点在同一个球面上 -
科目: 来源: 题型:
查看答案和解析>>【题目】亳州某商场举行购物抽奖活动,规定每位顾客从装有编号为0,1,2,3四个相同小求的抽奖箱中,每次取出一球,记下编号后放回,连续取两次,若取出的两个小球号码相加之和等于6,则中一等奖;等于5中二等奖;等于4或3中三等奖.
(1)求中三等奖的概率;
(2)求不中奖的概率.
相关试题

