【题目】在正项等比数列{an}中, ![]() ,a6+a7=3,则满足a1+a2+…+an>a1a2…an的最大正整数n的值为 .
,a6+a7=3,则满足a1+a2+…+an>a1a2…an的最大正整数n的值为 .
参考答案:
【答案】12
【解析】解:设正项等比数列{an}首项为a1 , 公比为q,
由题意可得 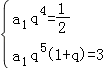 ,解之可得:a1=
,解之可得:a1= ![]() ,q=2,
,q=2,
故其通项公式为an= ![]() =2n﹣6 .
=2n﹣6 .
记Tn=a1+a2+…+an= ![]() =
= ![]() ,
,
Sn=a1a2…an=2﹣5×2﹣4…×2n﹣6=2﹣5﹣4+…+n﹣6= ![]() .
.
由题意可得Tn>Sn , 即 ![]() >
> ![]() ,
,
化简得:2n﹣1> ![]() ,即2n﹣
,即2n﹣ ![]() >1,
>1,
因此只须n> ![]() ,即n2﹣13n+10<0
,即n2﹣13n+10<0
解得 ![]() <n<
<n< ![]() ,
,
由于n为正整数,因此n最大为 ![]() 的整数部分,也就是12.
的整数部分,也就是12.
所以答案是:12
【考点精析】关于本题考查的解一元二次不等式和等差数列的前n项和公式,需要了解求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;前n项和公式:
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;前n项和公式:![]() 才能得出正确答案.
才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的奇函数.当x>0时,f(x)=x2﹣4x,则不等式f(x)>x 的解集用区间表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人各射击一次,击中目标的概率分别是
 和
和 .假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.(1)求甲射击4次,至少1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
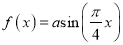 (
(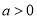 )在同一半周期内的图象过点
)在同一半周期内的图象过点 ,
,  ,
, 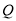 ,其中
,其中 为坐标原点,
为坐标原点, 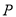 为函数
为函数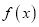 图象的最高点,
图象的最高点, 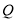 为函数
为函数 的图象与
的图象与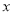 轴的正半轴的交点,
轴的正半轴的交点, 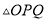 为等腰直角三角形.
为等腰直角三角形.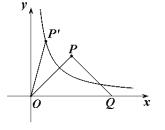
(1)求
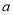 的值;
的值;(2)将
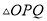 绕原点
绕原点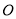 按逆时针方向旋转角
按逆时针方向旋转角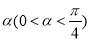 ,得到
,得到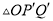 ,若点
,若点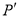 恰好落在曲线
恰好落在曲线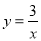 (
( )上(如图所示),试判断点
)上(如图所示),试判断点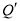 是否也落在曲线
是否也落在曲线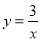 (
(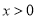 )上,并说明理由.
)上,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 =(cosα,sinα),
=(cosα,sinα),  =(cosβ,sinβ),0<β<α<π.
=(cosβ,sinβ),0<β<α<π.
(1)若| ﹣
﹣  |=
|=  ,求证:
,求证:  ⊥
⊥  ;
;
(2)设 =(0,1),若
=(0,1),若  +
+  =
=  ,求α,β的值.
,求α,β的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥S﹣ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.求证:

(1)平面EFG∥平面ABC;
(2)BC⊥SA. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x﹣4.设圆C的半径为1,圆心在l上.

(1)若圆心C也在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
相关试题

