【题目】甲、乙两人各射击一次,击中目标的概率分别是![]() 和
和![]() .假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
(1)求甲射击4次,至少1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率.
参考答案:
【答案】(1) ![]() .
.
(2) ![]() .
.
【解析】分析:(I)设“甲射击5次,至少1次未击中目标”为事件![]() ,则其对立事件
,则其对立事件![]() 为“4次均击中目标”,通过间接法,由n次独立重复事件恰好发生k次的概率公式计算可得答案;(Ⅱ)设“两人各射击4次,甲恰好击中目标2次,且乙恰好击中目标3次”为事件B,分别计算甲恰好击中目标2次的概率与乙恰好击中目标3次的概率,再由独立事件的概率的计算公式,计算可得答案.
为“4次均击中目标”,通过间接法,由n次独立重复事件恰好发生k次的概率公式计算可得答案;(Ⅱ)设“两人各射击4次,甲恰好击中目标2次,且乙恰好击中目标3次”为事件B,分别计算甲恰好击中目标2次的概率与乙恰好击中目标3次的概率,再由独立事件的概率的计算公式,计算可得答案.
详解:
(1)设“甲射击4次,至少1次未击中目标”为事件![]() ,
,
则其对立事件![]() 为“4次均击中目标”,
为“4次均击中目标”,
则![]() ;
;
(2)设“甲恰好击中目标2次且乙恰好击中目标3次”为事件![]() ,
,
则![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x
1.08
1.12
1.19
1.28
1.36
1.48
1.59
1.68
1.80
1.87
y
2.25
2.37
2.40
2.55
2.64
2.75
2.92
3.03
3.14
3.26
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:
 ,
, ,
,②参考公式:相关系数
 ,
,回归方程
 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:
运动员
第一次
第二次
第三次
第四次
第五次
甲
87
91
90
89
93
乙
89
90
91
88
92
则成绩较为稳定(方差较小)的那位运动员成绩的方差为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的奇函数.当x>0时,f(x)=x2﹣4x,则不等式f(x)>x 的解集用区间表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
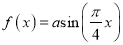 (
(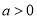 )在同一半周期内的图象过点
)在同一半周期内的图象过点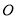 ,
,  ,
, 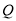 ,其中
,其中 为坐标原点,
为坐标原点, 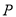 为函数
为函数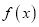 图象的最高点,
图象的最高点, 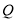 为函数
为函数 的图象与
的图象与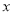 轴的正半轴的交点,
轴的正半轴的交点,  为等腰直角三角形.
为等腰直角三角形.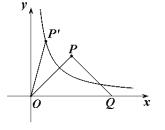
(1)求
 的值;
的值;(2)将
 绕原点
绕原点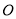 按逆时针方向旋转角
按逆时针方向旋转角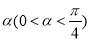 ,得到
,得到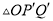 ,若点
,若点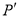 恰好落在曲线
恰好落在曲线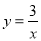 (
( )上(如图所示),试判断点
)上(如图所示),试判断点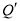 是否也落在曲线
是否也落在曲线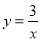 (
(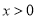 )上,并说明理由.
)上,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正项等比数列{an}中,
 ,a6+a7=3,则满足a1+a2+…+an>a1a2…an的最大正整数n的值为 .
,a6+a7=3,则满足a1+a2+…+an>a1a2…an的最大正整数n的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 =(cosα,sinα),
=(cosα,sinα),  =(cosβ,sinβ),0<β<α<π.
=(cosβ,sinβ),0<β<α<π.
(1)若| ﹣
﹣  |=
|=  ,求证:
,求证:  ⊥
⊥  ;
;
(2)设 =(0,1),若
=(0,1),若  +
+  =
=  ,求α,β的值.
,求α,β的值.
相关试题

