【题目】已知等差数列{an}的首项为a,公差为b,方程ax2-3x+2=0的解为1和b,
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an·2n,求数列{bn}的前n项和Tn.
参考答案:
【答案】(1) an=2n-1(2) Tn=(2n-3)·2n+1+6
【解析】试题分析:(1)由方程ax2-3x+2=0的两根为x1=1,x2=b代入方程可得![]() 求出
求出![]() ,求得
,求得![]() ;(2)由(1)得bn=(2n-1)2n,由此利用错位相减法能够求出数列{bn}的前n项和Tn.
;(2)由(1)得bn=(2n-1)2n,由此利用错位相减法能够求出数列{bn}的前n项和Tn.
试题解析:
(1)因为方程ax2-3x+2=0的两根为x1=1,x2=b,
可得![]() ,故a=1,b=2.所以an=2n-1.
,故a=1,b=2.所以an=2n-1.
(2)由(1)得bn=(2n-1)·2n,
所以Tn=b1+b2+…+bn=1·2+3·22+…+(2n-1)·2n, ①
2Tn=1·22+3·23+…+(2n-3)·2n+(2n-1)·2n+1, ②
②-①得
Tn=-2(2+22+…+2n)+(2n-1)·2n+1+2=(2n-3)·2n+1+6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南
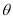 方向
方向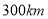 的海面P处,且
的海面P处,且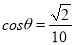 ,并以
,并以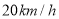 的速度向西偏北
的速度向西偏北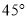 方向移动,台风侵袭的范围为圆形区域,当前半径为
方向移动,台风侵袭的范围为圆形区域,当前半径为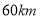 ,并以
,并以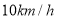 的速度不断增大,问几小时后该城市开始受到台风的侵袭?
的速度不断增大,问几小时后该城市开始受到台风的侵袭?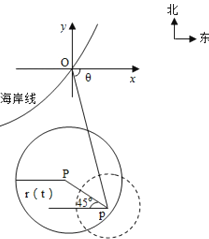
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
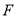 是拋物线
是拋物线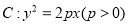 的焦点, 若点
的焦点, 若点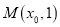 在
在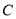 上,且
上,且 .
.(1)求
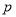 的值;
的值;(2)若直线
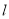 经过点
经过点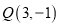 且与
且与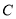 交于
交于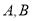 (异于
(异于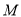 )两点, 证明: 直线
)两点, 证明: 直线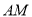 与直线
与直线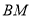 的斜率之积为常数.
的斜率之积为常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax+
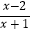 (a>1)
(a>1)
(1)证明:函数f(x)在(﹣1,+∞)上为增函数;
(2)用反证法证明f(x)=0没有负数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=
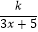 (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式.
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
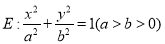 过点
过点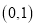 ,且离心率为
,且离心率为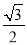 .
.(Ⅰ)求椭圆
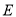 的方程;
的方程;(Ⅱ)设直线
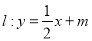 与椭圆
与椭圆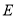 交于
交于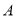 、
、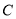 两点,以
两点,以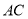 为对角线作正方形
为对角线作正方形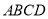 ,记直线
,记直线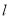 与
与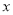 轴的交点为
轴的交点为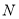 ,问
,问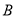 、
、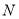 两点间距离是否为定值?如果是,求出定值;如果不是,请说明理由.
两点间距离是否为定值?如果是,求出定值;如果不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣x3+ax2+bx+c图象上的点P(1,m)处的切线方程为y=﹣3x+1
(1)若函数f(x)在x=﹣2时有极值,求f(x)的表达式.
(2)若函数f(x)在区间[﹣2,0]上单调递增,求实数b的取值范围.
相关试题

