【题目】已知圆![]() ,直线
,直线![]() ,
, ![]() .
.
(1)求证:对![]() ,直线
,直线![]() 与圆
与圆![]() 总有两个不同的交点
总有两个不同的交点![]() ;
;
(2)求弦![]() 的中点
的中点![]() 的轨迹方程,并说明其轨迹是什么曲线;
的轨迹方程,并说明其轨迹是什么曲线;
(3)是否存在实数![]() ,使得原
,使得原![]() 上有四点到直线
上有四点到直线![]() 的距离为
的距离为![]() ?若存在,求出
?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
参考答案:
【答案】(1)见解析;(2)M的轨迹方程是![]() ,它是一个以
,它是一个以![]() 为圆心,以
为圆心,以![]() 为半径的圆;(3)
为半径的圆;(3)![]() 或
或![]() .
.
【解析】【试题分析】(1)依据题设可以运用圆心与直线的距离或考虑动直线过定点分析判断;(2)借助题设条件运用圆心与弦中点的连线与直线垂直建立方程求解;(3)依据题设借助图形的直观,运用圆心距与直线的位置和数量关系建立不等式:
(1)圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,所以圆心C到直线
,所以圆心C到直线![]() 的距离
的距离 .
.
所以直线![]() 与圆C相交,即直线
与圆C相交,即直线![]() 与圆
与圆![]() 总有两个不同的交点;
总有两个不同的交点;
或:直线![]() 的方程可化为
的方程可化为![]() ,无论m怎么变化,直线
,无论m怎么变化,直线![]() 过定点
过定点![]() ,由于
,由于![]() ,所以点
,所以点![]() 是圆C内一点,故直线
是圆C内一点,故直线![]() 与圆
与圆![]() 总有两个不同的交点.
总有两个不同的交点.
(2)设中点为![]() ,因为直线
,因为直线![]() 恒过定点
恒过定点![]() ,
,
当直线![]() 的斜率存在时,
的斜率存在时, ![]() ,又
,又![]() ,
, ![]() ,
,
所以![]() ,化简得
,化简得![]() .
.
当直线![]() 的斜率不存在时,中点
的斜率不存在时,中点![]() 也满足上述方程.
也满足上述方程.
所以M的轨迹方程是![]() ,它是一个以
,它是一个以![]() 为圆心,以
为圆心,以![]() 为半径的圆.
为半径的圆.
(3) 假设存在直线![]() ,使得圆上有四点到直线
,使得圆上有四点到直线![]() 的距离为
的距离为![]() ,由于圆心
,由于圆心![]() ,半径为
,半径为![]() ,则圆心
,则圆心![]() 到直线
到直线![]() 的距离为
的距离为
化简得![]() ,解得
,解得![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一鲜花店一个月(30天)某种鲜花的日销售量与销售天数统计如下:
日销售量(枝)
0~49
50~99
100~149
150~199
200~250
销售天数(天)
3天
3天
15天
6天
3天
将日销售量落入各组区间的频率视为概率.
(1)试求这30天中日销售量低于100枝的概率;
(2)若此花店在日销售量低于100枝的6天中选择2天作促销活动,求这2天的日销售量都低于50枝的概率(不需要枚举基本事件).
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn,n∈N*.已知a1=1,a2=
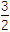 ,a3=
,a3=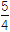 ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.(1)求a4的值;
(2)证明:
 为等比数列;
为等比数列;(3)求数列{an}的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数f(x)是奇函数,且满足f(x)=f(x+3),f(-2)=-3.若数列{an}中,a1=-1,且前n项和Sn满足
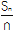 =2×
=2×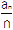 +1,则f(a5)+f(a6)=________.
+1,则f(a5)+f(a6)=________. -
科目: 来源: 题型:
查看答案和解析>>【题目】分形几何学是数学家伯努瓦·曼德尔布罗在
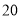 世纪
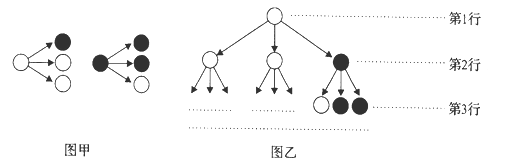
世纪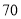 年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图所示的分形规律可得如图乙所示的一个树形图:
年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图所示的分形规律可得如图乙所示的一个树形图:若记图乙中第
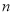 行白圈的个数为
行白圈的个数为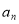 ,则
,则 __________.
__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为确立下一年度投入某种产品的宣传费,需了解年宣传费
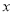 (单位:千元)对年销售量
(单位:千元)对年销售量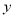 (单位:
(单位:  )和年利润
)和年利润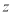 (单位:千元)的影响.对近
(单位:千元)的影响.对近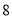 年的宣传费
年的宣传费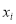 和年销售量
和年销售量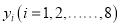 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.表中
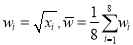

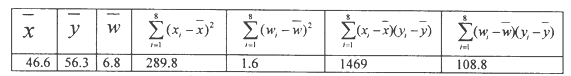
(Ⅰ)根据散点图判断,
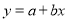 与
与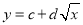 哪一个适宜作为年销售量
哪一个适宜作为年销售量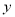 关于年宣传费
关于年宣传费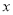 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立
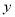 关于
关于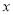 的回归方程;
的回归方程;(Ⅲ)已知这种产品的年利率
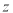 与
与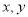 的关系为
的关系为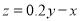 .根据(Ⅱ)的结果回答下列问题:
.根据(Ⅱ)的结果回答下列问题:(i)年宣传费
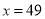 时,年销售量及利润的预报值是多少?
时,年销售量及利润的预报值是多少?(ii)年宣传费
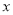 为何值时,年利率的预报值最大?
为何值时,年利率的预报值最大?附:对于一组数据
 ……
……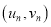 ,其回归线
,其回归线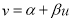 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为:  ,
, 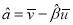
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是 ,
,  是
是 的中点.
的中点.
(1)求证:
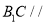 平面
平面 ;
;(2)求二面角
 的大小;
的大小;(3)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
相关试题

