【题目】一鲜花店一个月(30天)某种鲜花的日销售量与销售天数统计如下:
日销售量(枝) | 0~49 | 50~99 | 100~149 | 150~199 | 200~250 |
销售天数(天) | 3天 | 3天 | 15天 | 6天 | 3天 |
将日销售量落入各组区间的频率视为概率.
(1)试求这30天中日销售量低于100枝的概率;
(2)若此花店在日销售量低于100枝的6天中选择2天作促销活动,求这2天的日销售量都低于50枝的概率(不需要枚举基本事件).
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由互斥事件的概率加法公式得: ![]()
![]() ;(2)由古典概型的概率计算公式,所求概率
;(2)由古典概型的概率计算公式,所求概率![]() .
.
试题解析:(1)设日销售量为![]() ,则
,则![]() ,
, ![]() .
.
由互斥事件的概率加法公式,
![]()
![]() .
.
注:直接按照古典概型的计算公式,得![]() .同样给分.
.同样给分.
(2)日销售量低于100枝共有6天,从中任选两天促销共有![]() 种情况;日销售量低于50枝共有3天,从中任选两天促销共有
种情况;日销售量低于50枝共有3天,从中任选两天促销共有![]() 种情况.
种情况.
由古典概型的概率计算公式,所求概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:

(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附:
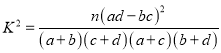 ,
, 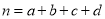 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax+x2-xlna,a>1.
(1)求证:函数f(x)在(0,+∞)上单调递增;
(2)对任意x1,x2∈[-1,1],|f(x1)-f(x2)|≤e-1恒成立,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】公元
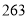 年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值
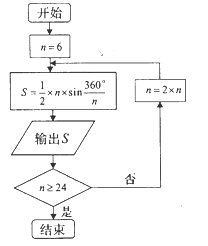
年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值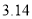 ,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中
,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中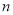 表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为 ( )
表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为 ( )(参考数据:
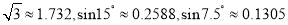 )
)
A. 2.598,3,3.1048 B. 2.598,3,3.1056
C. 2.578,3,3.1069 D. 2.588,3,3.1108
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn,n∈N*.已知a1=1,a2=
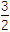 ,a3=
,a3=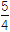 ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.(1)求a4的值;
(2)证明:
 为等比数列;
为等比数列;(3)求数列{an}的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数f(x)是奇函数,且满足f(x)=f(x+3),f(-2)=-3.若数列{an}中,a1=-1,且前n项和Sn满足
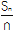 =2×
=2×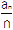 +1,则f(a5)+f(a6)=________.
+1,则f(a5)+f(a6)=________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
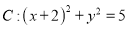 ,直线
,直线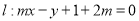 ,
, 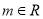 .
.(1)求证:对
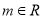 ,直线
,直线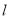 与圆
与圆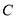 总有两个不同的交点
总有两个不同的交点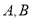 ;
;(2)求弦
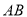 的中点
的中点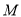 的轨迹方程,并说明其轨迹是什么曲线;
的轨迹方程,并说明其轨迹是什么曲线;(3)是否存在实数
 ,使得原
,使得原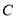 上有四点到直线
上有四点到直线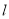 的距离为
的距离为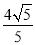 ?若存在,求出
?若存在,求出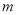 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
相关试题

