【题目】已知 ![]() ,
, ![]() ,当k为何值时,
,当k为何值时,
(1)![]() 与
与 ![]() 垂直?
垂直?![]()
(2)![]() 与
与 ![]() 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?![]()
参考答案:
【答案】
(1)
解:k ![]()
![]() =(1,2)﹣3(﹣3,2)=(10,﹣4)
=(1,2)﹣3(﹣3,2)=(10,﹣4)
![]() ,得
,得 ![]() =10(k﹣3)﹣4(2k+2)=2k﹣38=0,k=19
=10(k﹣3)﹣4(2k+2)=2k﹣38=0,k=19
(2)
解: ![]() ,得﹣4(k﹣3)=10(2k+2),k=﹣
,得﹣4(k﹣3)=10(2k+2),k=﹣ ![]()
此时k ![]() (10,﹣4),所以方向相反
(10,﹣4),所以方向相反
【解析】先求出 ![]() 的坐标,(1)利用向量垂直的充要条件:数量积为0,列出方程求出k.(2)利用向量共线的坐标形式的充要条件:坐标交叉相乘相等,列出方程求出k,将k代入两向量的坐标,判断出方向相反.
的坐标,(1)利用向量垂直的充要条件:数量积为0,列出方程求出k.(2)利用向量共线的坐标形式的充要条件:坐标交叉相乘相等,列出方程求出k,将k代入两向量的坐标,判断出方向相反.
【考点精析】解答此题的关键在于理解数量积判断两个平面向量的垂直关系的相关知识,掌握若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ;即:两平面垂直
;即:两平面垂直![]() 两平面的法向量垂直.
两平面的法向量垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为
 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:交强险浮动因素和浮动费率比率表
浮动因素
浮动比率

上一个年度未发生有责任道路交通事故
下浮10%

上两个年度未发生责任道路交通事故
下浮20%

上三个及以上年度未发生有责任道路交通事故
下浮30%

上一个年度发生一次有责任不涉及死亡的道路交通事故
0%

上一个年度发生两次及两次以上有责任道路交通事故
上浮10%

上一个年度发生有责任道路交通死亡事故
上浮30%
某机购为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型






数量
10
5
5
20
15
5
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事用户车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有六辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两辆车恰好有一辆为事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
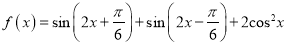 .
.(Ⅰ)
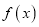 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;(Ⅱ)已知a,b,c是△ABC三边长,且f(C)=2,△ABC的面积S=
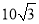 ,c=7.求角C及a,b的值.
,c=7.求角C及a,b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
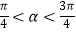 ,0<β<
,0<β<  ,cos(
,cos(  +α)=﹣
+α)=﹣ 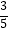 ,sin(
,sin( 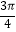 +β)=
+β)= 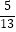 ,求sin(α+β)的值.
,求sin(α+β)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】.(本小题满分12分)
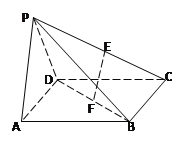
如图,四棱锥P—ABCD中,底面ABCD是边长为
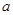 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=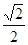 AD.
AD.(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 =(
=( 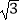 sinx,m+cosx),
sinx,m+cosx), 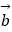 =(cosx,﹣m+cosx),且f(x)=
=(cosx,﹣m+cosx),且f(x)= 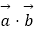
(1)求函数f(x)的解析式;
(2)当x∈[﹣ ,
,  ]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值.
]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值,并求出相应的x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
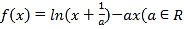 且
且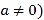
(1)讨论
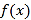 的单调区间;
的单调区间;(2)若直线
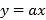 的图象恒在函数
的图象恒在函数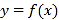 图象的上方,求
图象的上方,求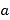 的取值范围.
的取值范围.
相关试题

